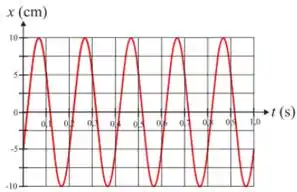
O gráfico mostra a posição em função do tempo de uma partícula de massa , ligada a uma mola de massa desprezível, que move-se em movimento retilíneo, sobre uma mesa horizontal lisa, na direção do eixo x, orientado para a direita.
. Se o movimento realizado pela massa é um e a sua posição de equilíbrio ocorre em , podemos afirmar que a expressão da posição da partícula em função do tempo,
no sistema , é dada por:
Passo 1
Vem comigo que a gente vai detonar essa questão.
Temos um sistema com em mãos. Para encontrar a expressão que descreve a posição da partícula, vamos usar o fato de que a equação geral de um é dada por:
Onde é a amplitude do movimento, onde ( período) e é a fase do movimento.
Então temos que achar esses parâmetros para a nossa situação.
Passo 2
Vamos então encontrar esses parâmetros.
A amplitude é dada pela posição máxima da partícula, olhando o gráfico vemos que .
A gora vamos encontrar , temos o seguinte:
Para fazer essa conta temos que achar o período. Período é o tempo que se leva para ter uma oscilação, olhando o gráfico temos oscilações em um segundo, logo:
Com isso temos que:
Passo 3
Agora temos que encontrar a fase . Para isso vamos usar a condição inicial da partícula, já que olhando o gráfico temos que em , . Assim usando o que temos até agora na expressão da posição.
Com isso temos que:
Ou
Mas qual é correto? Então, vamos usar outra informação do enunciado, ele diz que em a partícula começa seu movimento na direção positivo, então temos que . Usando que , temos:
Para que essa velocidade seja positiva temos que e para que isso seja verdade temos que .
Agora juntando tudo a nossa expressão fica da seguinte forma:
Então a alternativa correta é a letra .