Um solenoide muito longo, coaxial com o eixo , tem comprimento , raio e espiras no total. O solenoide é colocado no vácuo. Desprezando efeitos de borda, o campo dentro do solenoide é , onde é a corrente através das espiras.
(a) (1,0 ponto) Calcula a indutância do solenoide.
(b) (1,5 ponto) Uma corrente variável no tempo dada por percorre o solenoide. Usando a lei de Faraday, calcule o vetor campo elétrico na região , onde é a distância ao eixo do solenoide.
Passo 1
Vamos, inicialmente, entender qual é a direção do campo elétrico . Bem, a lei de Lenz nos diz que a corrente induzida pela variação do campo magnético é contrária a já existente. Afinal de contas, a natureza busca um equilíbrio! Se a corrente induzida tivesse o mesmo sentido da corrente que passa pelas bobinas, elas se somariam e induziriam uma nova corrente na mesma direção, entrando em um ciclo sem fim.
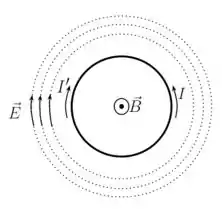
Sabemos, também, que o sentido do campo é o mesmo da corrente. Ou seja, o campo elétrico induzido irá possuir o mesmo sentido da corrente induzida, que é contrária à original. Vamos visualizar isso na figura abaixo para ficar mais claro!
Passo 2
Temos o sentido, agora precisamos calcular o módulo! Para isso, utilizamos diretamente a lei de Faraday, que diz:
No item (a), calculamos o fluxo , que é dado por:
Passo 3
Assim sendo, o lado direito da lei de Faraday se torna:
Substituindo o valor de , temos:
Passo 4
Do lado esquerdo da lei de Faraday, temos:
Passo 5
Comparando os dois lados, temos:
Resposta
O módulo do campo elétrico na região é dado por:
Sua direção pode ser vista na figura apresentada no Passo 1.