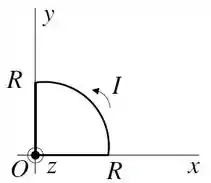
(I) (1,0 ponto) Uma espira plana, contida no plano , é constituída de um segmento circular de raio e dois segmentos retos de comprimento , conforme a figura. Pela espira flui o sentido anti-horário uma corrente . Calcule o vetor campo magnético produzido pela espira no ponto (origem do sistema de coordenadas).
Passo 1
Podemos calcular o campo magnético pedido no item (I) utilizando, inicialmente, a lei de Biot e Savart, dada por:
Em seguida, calculamos a integral em todos os segmentos que conduzem a corrente para obtermos .
Passo 2
A espira possui três principais regiões: dois segmentos retos e um terceiro dado por um quarto de circunferência.
Para os segmentos retos, e são paralelos, o que significa que seu produto vetorial é nulo. Portanto, estes segmentos não vão colaborar para o cálculo do campo magnético.
Passo 3
Agora, vamos olhar para a figura a seguir para analisar a terceira região, constituída do quarto de circunferência.
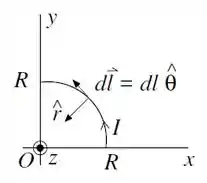
Bem, somos capazes de perceber que, nesse caso, e são ortogonais entre si. Pela regra da mão direita, temos:
A partir da equação de Biot e Savart, temos:
Passo 4
Finalmente, integramos a equação acima para calcular :
Resposta
O vetor campo magnético é dado por: