(II) A figura abaixo mostra a seção reta de uma casca cilíndrica muito longa de raio interno e raio externo , coaxial com o eixo . Pela casca flui, na direção positiva do eixo (direção saindo do papel), uma corrente uniformemente distribuída através de sua seção reta.
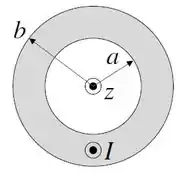
(a) (0,5 ponto) Calcule o vetor densidade de corrente na região , onde é a distância ao eixo da casca cilíndrica.
(b) (1,0 ponto) Calcule o vetor campo magnético na região .
Passo 1
Para o cálculo do campo magnético na região , vamos utilizar a lei de Ampère.
Bem, a lei de Ampère nos diz que:
onde é a corrente resultante do interior do percurso.
Vamos descobrir, antes de tudo, a direção do campo magnético . Bem, do enunciado, sabemos que a corrente flui na direção do eixo , que sai do plano da folha. Pela regra da mão direta, percebemos que o campo gira em torno da casca cilíndrica, como na figura abaixo.
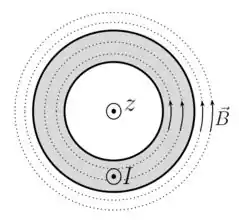
Passo 2
Mas e agora, qual percurso escolher? Vamos prestar atenção na figurinha aqui de baixo.

Se escolhermos o percurso tracejado de raio , o campo estará alinhado com o segmento vetorial do percurso . Opa! E isso é bom, porque facilita na conta do produto escalar que tem dentro da integral de linha.
Só mais um detalhe: o campo magnético varia de acordo com o raio escolhido e, portanto, vamos escrever no lugar de simplesmente a partir de agora.
Passo 3
Escolhemos o percurso, agora vamos usar a lei de Ampère para calcular o campo . Do lado esquerdo da equação, temos:
Para o lado direito, precisamos calcular primeiro a corrente interna Sabemos o valor da densidade de corrente, calculada no item anterior. Para calcular , fazemos:
onde é a área da casca cilíndrica de raio , dada por . Temos:
Assim, do lado direito da equação, teremos:
Por fim, igualamos os dois lados para obter o módulo de :
Resposta
O módulo do campo magnético na região é dado por:
Sua direção pode ser vista na figura apresentada no Passo 1.