Listas de Física I da UFF - Lista 12 - Exercícios

Qual é o módulo e a direção do momento angular de um disco homogêneo de massa 2,0 kg e diâmetro 4,0 cm girando com velocidade angular ω = 100 rad/s em torno de um eixo perpendicular ao seu plano e que passa pelo seu centro?

Qual a energia cinética de rotação da Terra? Os dados sobre a Terra podem ser encontrados em qualquer livro de física básica.

Calcule o produto vetorial e entre os vetores mostrados nas figuras.

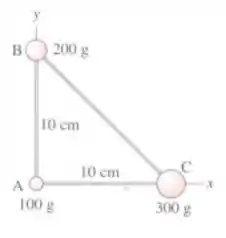
As três massas mostradas na figura estão conectadas por hastes rígidas de massas desprezíveis. Determine as coordenadas do centro de massa do sistema.

O objeto (sem massa) mostrado na figura está em equilíbrio? Explique.

Um disco fino, homogêneo, de massa 100 g e 8,0 cm de diâmetro gira em torno de um eixo perpendicular ao seu plano que passa pelo seu centro. A energia cinética de rotação do disco é de 0,15 J. Qual o módulo da velocidade de um ponto na borda do disco?

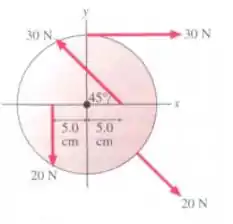
O disco de 20 cm de diâmetro mostrado na figura pode girar em torno do eixo que passa pelo seu centro, perpendicular ao disco, com atrito desprezível. As forças mostradas na figura estão aplicadas sobre o disco. Qual o torque resultante sobre o disco em torno do eixo mencionado?

Os blocos de massas e estão conectados por uma corda sem massa que passa por uma polia, como mostrado na figura. A polia é um disco homogêneo que pode girar em torno do seu eixo sem atrito. A massa desliza sem atrito sobre uma superfície horizontal. Os dois blocos estão em repouso quando a massa é liberada.

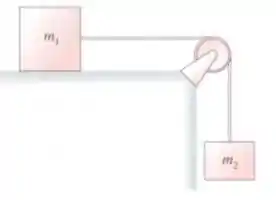
a) suponha que a massa da polia seja desprezível. Encontre as acelerações dos blocos e e a tensão na corda.

b) Suponha agora que a massa da polia é e seu raio é R. Encontre a aceleração de e as tensões nas partes vertical e horizontal da corda. Verifique que seus resultados condizem com os obtidos no item a) quando você faz =0

Uma viga metálica de 400 kg e 4 m de comprimento estende-se horizontalmente, perpendicular à parede onde está presa. Um trabalhador de massa 70 kg está sentado na extremidade livre da viga. Qual o torque total sobre a viga em torno do ponto onde ela está presa na parede?

Uma porta retangular homogênea de 25 kg tem 220 cm de altura e 91 cm de largura. Qual o momento de inércia da porta para rotações em torno de:

a) um eixo paralelo o seu lado mais longo que passa pelas dobradiças

b) um eixo paralelo ao seu lado mais longo que passa a uma distância de 15 cm das suas dobradiças.

Uma bola de 1,0 kg e uma bola de 2,0 kg, presas por um bastão rígido de 1,0 m de comprimento e massa desprezível, giram em torno do centro de massa do sistema no sentido horário a 20 rotações por minuto. Qual o torque necessário para levar o sistema ao repouso em 5,0 s?

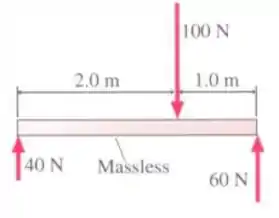
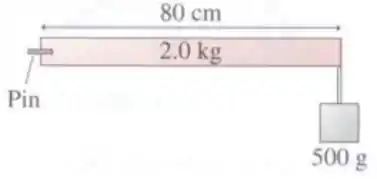
Que torque tem que ser exercido pelo pino na figura para evitar que o sistema gire?

A figura é um gráfico da posição angular (rad) do disco em rotação, no sentido indicado.

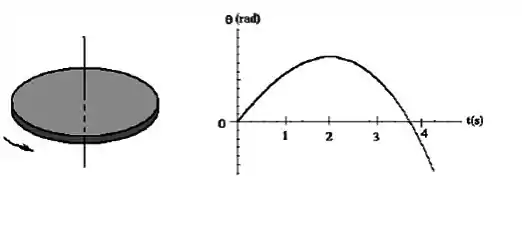
a) A velocidade angular do disco é positiva, negativa ou nula em t=0 s, t=1 s, t=2 s e t=3s.

b) A mesma pergunta do item a) para aceleração angular.

c) Indique na figura os vetores e nos instantes especificados.

Uma esfera de massa 400 g e raio 4 cm é liberada, a partir do repouso, do topo de uma rampa inclinada de 25º com relação à horizontal. A rampa tem comprimento de 2.1 m. A esfera rola sem deslizar até o fim da rampa.

a) Qual é a velocidade angular da esfera no final da rampa?

b) Qual fração da energia cinética da esfera é rotacional?

Calcule, por integração direta, o momento de inércia de um bastão de massa M e comprimento L em torno de um eixo que passa a uma distância d de uma de suas extremidades. Compare o seu resultado com tabelas de momentos de inércia para os casos particulares d=0 e d=L/2.

Um cilindro maciço de comprimento L e raio R tem peso P. Duas cordas são enroladas em torno do cilindro, perto de cada borda, e as pontas das cordas são presas a ganchos no teto. O cilindro é mantido na horizontal com as duas cordas exatamente verticais e então é abandonado.

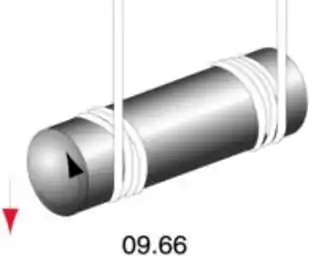
a) Faça o diagrama de forças sobre o cilindro.

b) Quais forças realizam trabalho durante a descida?

c) Calcule a tração em cada corda enquanto elas se desenrolam.

d) Calcule a aceleração linear do cilindro enquanto ele cai.

Na figura, um fio sem massa e inextensível passa sem escorregar ao redor da polia. Numa extremidade do fio é pendurado um bloco de massa m2 = 500 g, na outra, um bloco de massa m1 = 400 g, e a polia, que é um disco homogêneo montado num eixo horizontal sem atrito, tem um raio de 5,00 cm. Quando o sistema é abandonado a partir do repouso, o bloco de massa maior cai 75,0 cm e adquire uma velocidade linear de 30,0 cm/s.

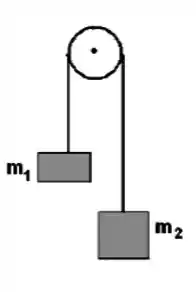
a) Faça os diagramas de força para cada bloco e polia.

b) Utilizando a conservação de energia mecânica determine a inércia rotacional da polia.

c) Determine o módulo e sentido da aceleração angular da polia.

d) Determine as tensões no fio e o vetor reação do eixo de rotação sobre a polia.

e) Qual é o vetor torque resultante em torno do eixo de rotação ? Faça dois cálculos, um utilizando a equação e outro .

f) Qual a força de atrito entre a corda e a polia?

Um aro circular de 60 cm de diâmetro está rolando sem deslizar sobre uma superfície plana. O módulo da velocidade do seu centro de massa é de 20 m/s. Qual o módulo da velocidade do ponto na extremidade frontal do aro?

Uma bolinha compacta de massa m e raio r rola sem deslizar ao longo do trilho em curva mostrado na figura abaixo, tendo sido abandonado em repouso em algum ponto da região reta do trilho.

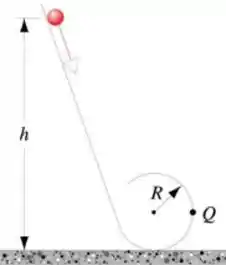
a) De que altura mínima h, a partir da base do trilho, a bolinha deve ser solta para eu percorra a parte superior da curva? (suponha que R>>r).

b) Se a bolinha for solta da altura 6R acima da base do trilho, qual a componente horizontal da força que atua sobre ela no ponto Q?

Um cubo de massa m, desliza sem atrito com velocidade . Ele então sofre uma colisão perfeitamente elástica com a extremidade inferior de uma haste de comprimento d e massa M=2m. A haste está presa a um eixo livre de atrito que passa por seu centro e, inicialmente, encontra-se na posição vertical, em repouso.

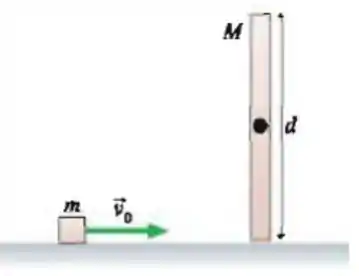
a) Que grandezas são conservadas na colisão?

b) Qual será a velocidade do cubo, módulo e orientação, após a colisão?