Uma bola de 1,0 kg e uma bola de 2,0 kg, presas por um bastão rígido de 1,0 m de comprimento e massa desprezível, giram em torno do centro de massa do sistema no sentido horário a 20 rotações por minuto. Qual o torque necessário para levar o sistema ao repouso em 5,0 s?
Passo 1
Temos nesse caso um corpo que possui uma velocidade angular inicial e deseja-se para-lo em um determinado tempo.
Para que esse corpo pare, é necessário uma aceleração angular contrária, que será gerado por um torque. A questão pede para se encontrar esse torque.
Sabemos que a segunda lei de newton para a rotação é:
Vamos começar encontrando o momento de inércia desse corpo.
Passo 2
Temos duas bolas presas por um bastão rígido. Para encontrarmos o momento de inércia em relação ao centro de massa, primeiro precisamos encontrar o seu centro de massa.
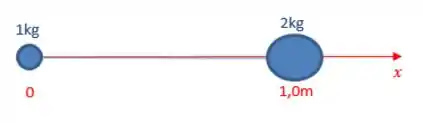
Para encontrar o centro de massa, eu escolhi um ponto para ser a origem e tracei o meu eixo x a partir dele. Agora é só jogar os valores na fórmula.
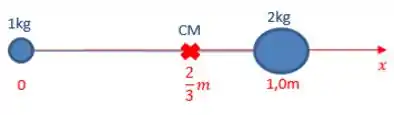
Conhecendo o centro de massa, agora eu consigo calcular o momento de inércia, considerando a massa de 1kg e a massa de 2kg como partículas:
Passo 3
Agora que encontramos o momento de inércia, precisamos saber qual deve ser a aceleração angular desse corpo.
A velocidade angular inicial dele foi dada como 20 rotações por minuto, passando para o SI teremos:
O enunciado pede que, com essa aceleração contrária, esse corpo pare em um tempo de 5s.
Podemos utilizar então a equação de variação da velocidade angular:
Encontramos uma aceleração angular pois ela é contrária a velocidade angular. O que faz TODO O SENTIDO, afinal essa é na verdade uma desaceleração.
Passo 4
Agora é só pegar esses valores de momento de inércia e de aceleração angular e colocar na segunda lei de newton para encontrarmos o torque!
Encontramos um valor negativo, o que indica que esse torque é contrário a velocidade angular. O que também faz TODO O SENTIDO, afinal esse torque está desacelerando o corpo.
Resposta
O módulo do torque necessário é 0,28Nm.