Uma bolinha compacta de massa m e raio r rola sem deslizar ao longo do trilho em curva mostrado na figura abaixo, tendo sido abandonado em repouso em algum ponto da região reta do trilho.
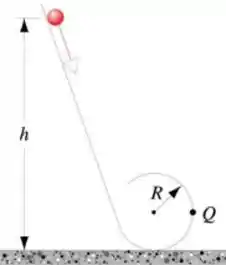
a) De que altura mínima h, a partir da base do trilho, a bolinha deve ser solta para eu percorra a parte superior da curva? (suponha que R>>r).
b) Se a bolinha for solta da altura 6R acima da base do trilho, qual a componente horizontal da força que atua sobre ela no ponto Q?
Passo 1
Quando a bolinha estiver no ponto mais alto da curva, as forças que atuam sobre ela são:
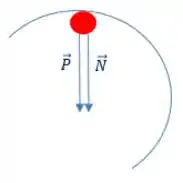
Podemos encontrar a força centrípeta como sendo:
Passo 2
Como, na letra a), queremos saber qual a altura mínima para que ela consiga percorrer a parte superior da curva, nós estamos trabalhando na iminência dela não conseguir realizar esse movimento.Que seria o mesmo que a bola perder o contato no ponto mais alto da curva.Logo a normal, é uma normal MUITO pequena, que tá indo pra zero, já que está na iminência de não conseguir realizar o movimento, por isso, consideraremos essa força normal como igual a zero.
Assim, teremos:
Agora, para relacionar a altura com que a bolinha foi largada com essa velocidade, é só realizar a conservação da energia mecânica. Antes, vamos dar uma olhada no desenho do movimento.
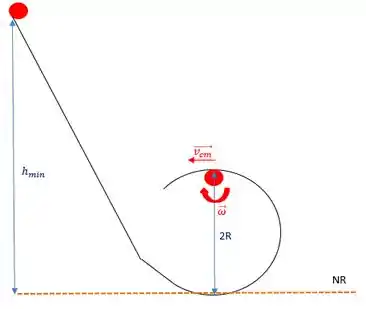
Teremos na conservação:
O momento de inércia de uma esfera ao redor do seu centro de massa é
Devemos também lembrar que no rolamento com deslizamento temos que , ou que .
Agora substituindo tudo isso, teremos:
Passo 3
Precisamos fazer novamente a conservação da energia, mas agora para o ponto onde a bolinha está na extremidade direita da curva.
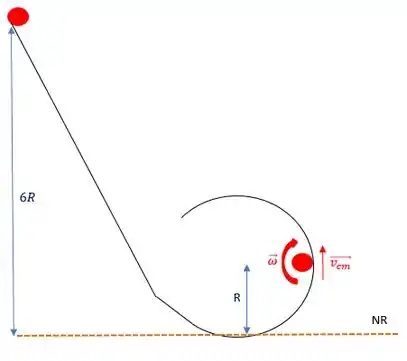
Passo 4
Analisando as forças que atuam sobre a bolinha quando ela passa pela extremidade direita, teremos:
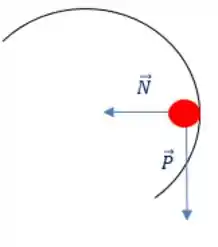
Daonde podemos avaliar que a força horizontal que atua sobre a bolinha é a força normal, e que essa força é a força centrípeta nesse movimento, afinal é a resultante que aponta para o centro do movimento.
Substituindo o valor da velocidade encontrada:
Resposta
a)
b)