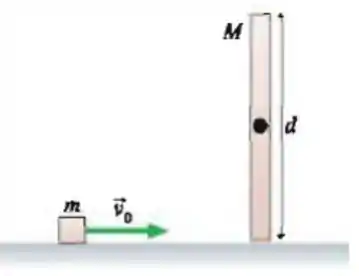
Um cubo de massa m, desliza sem atrito com velocidade . Ele então sofre uma colisão perfeitamente elástica com a extremidade inferior de uma haste de comprimento d e massa M=2m. A haste está presa a um eixo livre de atrito que passa por seu centro e, inicialmente, encontra-se na posição vertical, em repouso.
a) Que grandezas são conservadas na colisão?
b) Qual será a velocidade do cubo, módulo e orientação, após a colisão?
Passo 1
a)
Em uma colisão onde há rotação, podemos dizer que o momento angular se conserva, pois não há torques externos. Os únicos torque que atuam nessa colisão são o que a massa faz sobre a barra e o que a barra faz sobre a massa.
Também podemos falar que o momento linear se conserva, pois não há forças externas.
Como a natureza da colisão é elástica, podemos falar que a energia cinética se conserva.
Passo 2
b)
Mas o que vai realmente importar para a gente é a conservação do momento angular. Sempre que for colisão com rotação, você vai resolver pela conservação do momento angular, beleza?
Como a gente tá acostumado a fazer em uma colisão, vamos analisar o que está ocorrendo antes e depois da colisão:
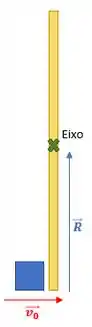
Antes da colisão, só temos velocidade para o bloco.
Com isso, o momento angular antes da colisão é:
E pela regra da mão direita (dada pelo produto vetorial ), vemos que esse momento angular está saindo da página ou anti-horário e vamos considerar esse sentido como o nosso positivo.
Agora pensando na nossa energia cinética, ela será:
Após o bloco bater na haste, ela entrará em movimento e teremos, após a colisão:
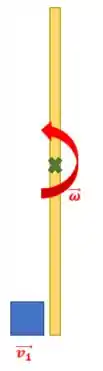
Repara que só podemos dizer a direção da velocidade angular da haste. Não sabemos se o bloco irá para a direita ou para a esquerda após a colisão, por enquanto.
O momento angular nesse caso ficará:
Sendo o momento de inércia de uma barra pelo seu centro de massa:
Agora a energia cinética (translacional para o bloco e rotacional para a barra) ficará:
Passo 3
Bom, esse passo agora é igualar os momentos angulares e as energias cinéticas.
Agora pensando na energia cinética, teremos:
Lembra de produtos notáveis, pois bem, vai usar agora rs... Bora substituir o que encontramos lá no momento angular.
Como , podemos dividir os dois lados por ele:
Eu já deixei esse em evidência na esperteza! Por que agora é só voltar lá na relação de momento angular inicial e final e substituir, saca só:
Encontramos o módulo da velocidade do bloco. Como esse valor, foi encontrado na equação como positivo, ele têm a mesma direção a velocidade , isso é , para a direita.
Resposta
b)
Para a direita.