Um disco fino, homogêneo, de massa 100 g e 8,0 cm de diâmetro gira em torno de um eixo perpendicular ao seu plano que passa pelo seu centro. A energia cinética de rotação do disco é de 0,15 J. Qual o módulo da velocidade de um ponto na borda do disco?
Passo 1
Primeiramente, vamos lembrar a fórmula da energia cinética de rotação:
Nesse caso, o disco roda ao redor de um eixo perpendicular que passa pelo seu centro, que por ser um disco homogêneo, é o seu centro de massa. O momento de inércia de um disco rodando ao redor do centro de massa é:
Com isso, teremos:
Daonde encontramos:
Passo 2
Podemos encontrar a velocidade em um ponto do disco pela relação:
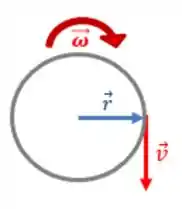
Onde é a distância do ponto com relação ao eixo de rotação, que no caso é o próprio raio do disco.
Resposta
Exercícios de Livros Relacionados
Uma régua de um metro é mantida verticalmente com uma das extremidades apoiada no solo e depois liberada. Determine a velocidade da outra extremidade pouco antes de tocar o solo, supondo que a extremi
Na figura abaixo, uma barra fina e homogênea (com 4 m de comprimento e uma massa de 3 k g ) gira livremente em torno de um eixo horizontal A que é perpendicular à barra e passa por um ponto situado a
O corpo rígido da figura abaixo é formado por três bolas e três barras de ligação, com M = 1,6 k g , L = 0,6 m e θ = 30 ° . As bolas podem ser tratadas como partículas e as barras têm massa desprezíve
Como estagiário de uma empresa de engenharia, você é solicitado a medir o momento de inércia de uma grande roda, para girar em torno de um eixo que passa pelo seu centro. Você mede o diâmetro da roda,
91 . Na F I G U R AP D 12.91 , uma bola de gude desce rolando um trilho que possui uma parte em loop com raio R . A bolinha possui massa m e raio r . Que altura mínima h deve ter o trilho a fim de que