Uma viga metálica de 400 kg e 4 m de comprimento estende-se horizontalmente, perpendicular à parede onde está presa. Um trabalhador de massa 70 kg está sentado na extremidade livre da viga. Qual o torque total sobre a viga em torno do ponto onde ela está presa na parede?
Passo 1
Primeiro passo aqui é a gente desenhar o que está rolando nesse exercício. Na verdade, sempre é bom desenhar para resolver questão de física!
Para calcularmos o torque, precisamos fazer o DCL sobre essa viga.
Passo 2
Fazendo um DCL, considerando o peso do trabalhador, o peso da viga e a normal que a parede faz sobre a viga para que ela não caia, teremos:
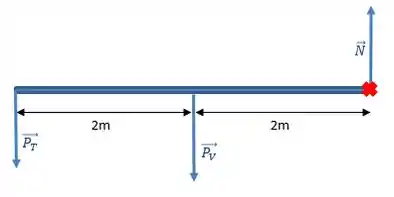
Repare que o peso da viga, nós colocamos atuando no seu centro de massa, que no caso, por ser uma viga homogênea, fica no seu meio.
Calculando o torque em relação ao ponto de contato da viga com a parede (marcado no DCL por um X) e considerando a direção para fora do papel (direção anti-horária) como positivo, teremos: