Calcule, por integração direta, o momento de inércia de um bastão de massa M e comprimento L em torno de um eixo que passa a uma distância d de uma de suas extremidades. Compare o seu resultado com tabelas de momentos de inércia para os casos particulares d=0 e d=L/2.
Passo 1
Beleza, pediu pra integrar, a gente integra... sem problemas!
Bom, primeiro passo é a gente desenhar um bastão de massa M e comprimento L, com o eixo a partir de uma de suas extremidades. Nesse bastão, vamos pegar um pedaço bem pequeno, finidesimal de massa dM e de largura dl.

Okay, agora vamos lembrar da fórmula do momento de inércia com integral:
E os intervalos de integração? Temos que ver como essa distância r pode variar. A esquerda do eixo, ela pode valer no máximo a distância d, e a direita do eixo, o seu valor máximo será igual a largura total da barra menos a distância d.
Passo 2
O enunciado se omite quanto a isso, mas iremos considerar a barra homogênea! Com isso podemos dizer que a relação entre um pedaço de massa com um pedaço de largura é a mesma entre a massa total e a largura total:
Substituindo teremos:
Passo 3
Beleza, finalmente encontramos o valor desse momento de inércia, agora vamos comparar com alguns valores tabelados, para ver se fizemos a conta certa, né.
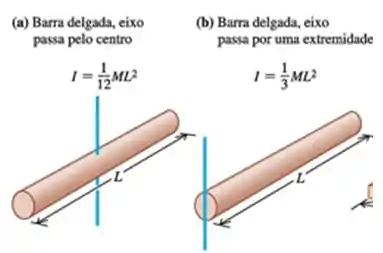
Utilizando d=0, temos o caso do momento de inércia de uma barra ao redor do eixo que passa pela sua extremidade.
Utilizando a expressão que encontramos, teremos
Que é igual ao valor da tabela!
Utilizando d=L/2, temos o caso do momento de inércia de uma barra ao redor do eixo que passa pelo seu centro de massa.
Utilizando a nossa expressão, teremos:
Que também é o valor tabelado! Ufa, parece que deu tudo certo!
