Um aro circular de 60 cm de diâmetro está rolando sem deslizar sobre uma superfície plana. O módulo da velocidade do seu centro de massa é de 20 m/s. Qual o módulo da velocidade do ponto na extremidade frontal do aro?
Passo 1
Primeiro, vamos dar uma desenhada nesse aro que está rolando, para vermos como ficam as velocidades em alguns dos seus pontos:
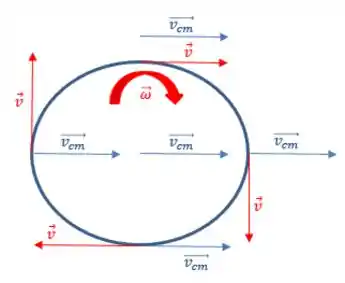
Como temos um rolamento sem deslizar, é necessário que a velocidade no ponto mais baixo do aro seja nula e assim temos que a velocidade do centro de massa é dada por:
Passo 2
Agora olhando só pro ponto na sua extremidade frontal:
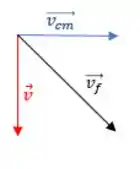
Por isso, o módulo da velocidade do ponto da extremidade frontal do aro é dada por:
Resposta
Exercícios de Livros Relacionados
Um mecanismo em forma de ioiô, montado em um eixo horizontal sem atrito, é usado para levantar uma caixa de 30kg , como mostra a figura abaixo. O raio externo R da roda é 0,5m e o raio r do cubo da ro
Na Fig. 11-60, uma força horizontal constante F → de módulo 12N é aplicada a um cilindro maciço homogêneo através de uma linha de pescar enrolada no cilindro. A massa do cilindro é 10k g , o raio é 0,
10.3E Um cilindro rola em uma rampa de inclinação θ = 30 ° . A) Calcule a aceleração angular do cilindro B) Calcule a força de atrito da rampa sobre o cilindro.
10.7P Calcule em termos do raio R da bola, o parâmetro de impacto b de uma tacada com que um jogador deve chutar uma bola para que esta tenha uma velocidade angular vertical dada por ω = v / 2 R .
Um ioiô possui um momento de inércia de 950 g c m ² ² e uma massa de 120 g . O raio do eixo é 3,2 m m e a corda tem 120 c m de comprimento. O ioiô rola para baixo, a partir do repouso, até a extremida