Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema dos Eixos Paralelos

Ver Teoria
Exercício 2312345678910111213141516171819202122242526272829

Enunciado

Uma porta retangular homogênea de 25 kg tem 220 cm de altura e 91 cm de largura. Qual o momento de inércia da porta para rotações em torno de:

a) um eixo paralelo o seu lado mais longo que passa pelas dobradiças

b) um eixo paralelo ao seu lado mais longo que passa a uma distância de 15 cm das suas dobradiças.

Passo 1

Primeiramente, temos que pensar que uma porta retangular pode ser visto como uma placa retangular e na tabela temos que:

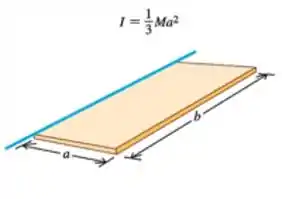
Então, para um eixo que é paralelo ao lado mais longo e que passa pela dobradiça da porta, temos o caso representado acima, onde o momento de inércia será:

I = 1 3 M a 2 = 1 3 * 25 * 0,91 2 = 6,90 k g m 2

Passo 2

Para encontrar o momento de inércia em relação ao eixo que está distante 15cm das dobradiças, precisamos usar o teorema dos eixos paralelos.

I o = I c m + M d 2

No entanto, é necessário conhecer o momento de inércia em relação ao centro de massa.

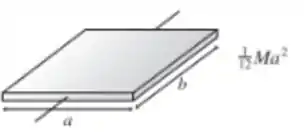
Que é dado pela tabela como sendo 1 12 M a 2 .

Para encontrar a distância do novo eixo com o eixo que passa pelo centro de massa, eu fiz esse esboço aqui rapidinho.

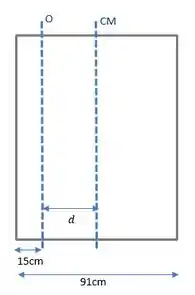
Onde vemos que

d = 91 2 - 15 = 30,5 c m

E portanto o momento de inércia em relação ao eixo O, que é o eixo pedido na letra b) é:

I o = 1 12 M a 2 + M d 2

I o = 1 12 * 25 * 0,91 2   +   25 * 0,305 2 =   4,05 k g m 2

Resposta

a)

I = 6,90 k g m 2

b)

I = 4,05 k g m 2

Exercícios de Livros Relacionados

Calcule o momento de inércia de um aro (um anel fino) de raio R e massa M em relação a um eixo perpendicular ao plano do aro passando pela sua periferia.
Um disco uniforme de raio r e massa M gira em torno de um eixo horizontal paralelo ao seu eixo de simetria e que passa por um ponto de seu perímetro, de forma a poder oscilar livremente em um plano ve
Usando o teorema dos eixos paralelos e informações da Tabela 9.2, ache o momento de inércia da barra delgada de massa M e comprimento L indicado na Figura 9.23 em relação a um eixo passando pelo ponto
Uma barra delgada de comprimento L possui massa por unidade de comprimento variando a partir da extremidade esquerda, onde x = 0 , de acordo com d m / d x = γ x , onde γ é constante com unidades de k
Use a Equação (9.20) para calcular o momento de inércia de um disco maciço, uniforme, de raio R e massa M em relação a um eixo perpendicular ao plano do disco passando pelo seu centro.