A figura é um gráfico da posição angular (rad) do disco em rotação, no sentido indicado.
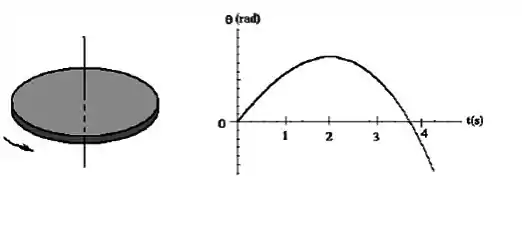
a) A velocidade angular do disco é positiva, negativa ou nula em t=0 s, t=1 s, t=2 s e t=3s.
b) A mesma pergunta do item a) para aceleração angular.
c) Indique na figura os vetores e nos instantes especificados.
Passo 1
Pensa comigo o seguinte, se fosse o caso linear essa questão estava tranquilona, né.
Por que aí é só lembrar que a velocidade é a derivada da posição e a aceleração é a derivada da velocidade.Se liga, isso também é válido para o movimento circular!

Passo 2
Então, olhando aí para o gráfico da posição angular, podemos traçar mais ou menos como ficaria o gráfico da velocidade angular, já que ele é a derivada da posição.
De cara, sabemos que o gráfico da velocidade angular cruza o eixo x em t=2s, pois nesse momento temos derivada igual a zero.
Olhando bem para o gráfico da posição angular, podemos perceber também que a derivada cresce até t=1s e depois decresce até t=2s (ponto aonde chega a zero).De t=2s em diante, esse derivada é negativa e está descrescendo cada vez mais.
Traçando então o gráfico da velocidade angular, vamos ter:
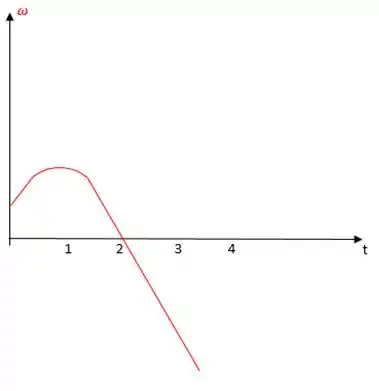
Logo, teremos que a velocidade angular é positiva para t=0 e t=1s. Ela é nula para t=2s. Ela é negativa para t=3s.
Passo 3
Agora para encontrar a aceleração angular? Bom para isso, vamos lembrar que a aceleração é a derivada da velocidade.
Para traçar o gráfico da aceleração, a gente pensa na derivada do gráfico anterior.
Sabemos que esse gráfico irá cruzar o eixo x em t=1s, pois é a derivada igual a zero do gráfico da velocidade angular. Vai ficar algo mais ou menos assim.
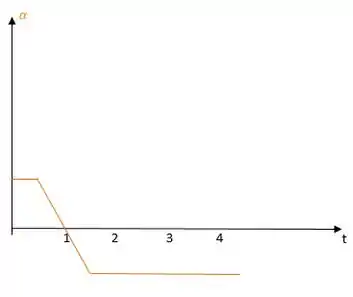
Por tanto, a aceleração angular é positiva para t=0s, nula em t=1s e negativa para t=2s e t=3s.
Passo 4
Agora só resta indicar os vetores velocidade e aceleração angular nos instantes indicados.
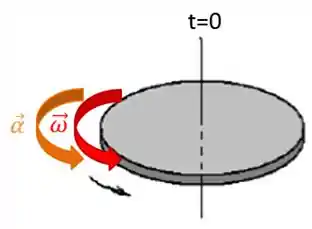
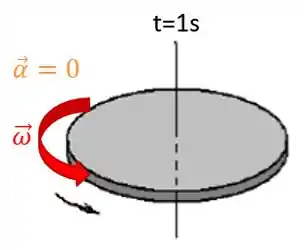
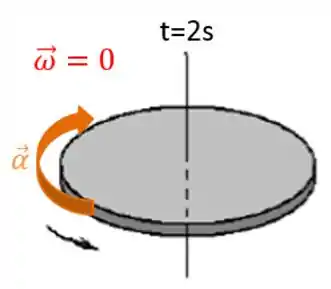
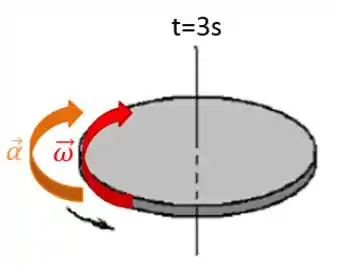
Resposta
a) Velocidade angular é positiva em t=0 e t=1s, nula em t=2s e negativa em t=3s.
b) Aceleração angular é positiva em t=0, nula em t=1s e negativa em t=2s e t=3s.