Qual é o módulo e a direção do momento angular de um disco homogêneo de massa 2,0 kg e diâmetro 4,0 cm girando com velocidade angular ω = 100 rad/s em torno de um eixo perpendicular ao seu plano e que passa pelo seu centro?

Como a rotação ocorre ao redor do centro de massa, utilizaremos o momento de inércia de um disco ao redor do seu centro de massa, que é tabelado:

Teremos portanto que o módulo de será:

Olhando para a equação

percebemos que tem a mesma direção e sentido que a velocidade angular .

Olhando para um disco que está rotacionando ao redor do eixo que passa pelo seu centro:

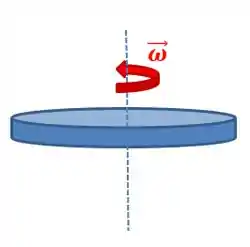
Pela regra da mão direita, vemos que a velocidade angular aponta para cima, ou seja, é na direção do eixo de rotação. Portanto, o momento angular   também terá essa direção.