Um cilindro maciço de comprimento L e raio R tem peso P. Duas cordas são enroladas em torno do cilindro, perto de cada borda, e as pontas das cordas são presas a ganchos no teto. O cilindro é mantido na horizontal com as duas cordas exatamente verticais e então é abandonado.
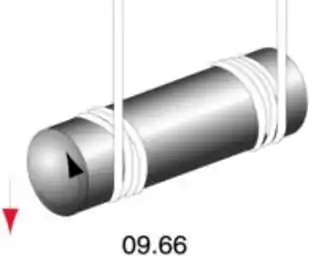
a) Faça o diagrama de forças sobre o cilindro.
b) Quais forças realizam trabalho durante a descida?
c) Calcule a tração em cada corda enquanto elas se desenrolam.
d) Calcule a aceleração linear do cilindro enquanto ele cai.
Passo 1
a)
Okay... temos um cilindo, ele gira pra um lado, desce pro outro... coisa de louco!
Mas vamos com calma, a letra a) pede o diagrama do corpo livre. Como esse cilindro é um objeto em três dimensões, vou fazer dois diagramas:
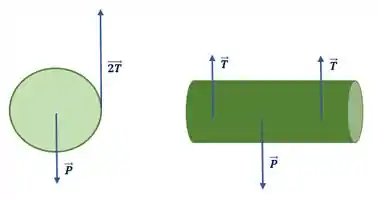
Repara que eu considerei que a tração nos dois cabos é a mesma. Se esse cilindro descer reto (sem inclinar) e a distância entre as cordas e o centro de massa for o mesmo, não tem jeito, tá tudo muito simétrico, logo as trações a gente considera como iguais.
Passo 2
b)
Se considerarmos que não há deslizamento entre a corda e o cilindro, podemos dizer que o atrito entre a corda e o cilindro é o atrito estático. O atrito estático não é capaz de realizar trabalho. Pensa comigo: trabalho é o produto escalar entre a força e o deslocamento, se no ponto onde há atrito estático não há movimento, logo não há trabalho.
Agora, a força peso não têm essa. Ela atua ali no centro de massa e ele está se movimentando (para baixo).
Por isso, a força que realiza trabalho é a força peso e apenas ela.
Passo 3
c)
Para a gente calcular a tração em cada corda, precisamos analisar esse movimento pelas leis de newton e considera-lo como sendo um rolamento sem deslizamento.
Quando a gente considera isso, a gente de cara já fala que:
Analisando a segunda lei de newton para translação conseguimos a aceleração do centro de massa () e a aceleração angular ().
Segunda lei para translação:
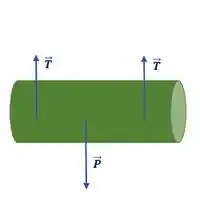
Encontrando a resultante e aplicando a segunda lei de Newton:
Segunda lei para rotação:
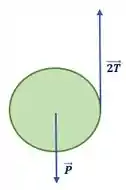
Vamos avaliar o torque resultante, em cima do nosso eixo de rotação (que é o centro de massa).
Como a força peso está aplicada bem no centro de massa, ela não realiza torque, só a força tração (das duas cordas). Vamos ter então:
O momento de inércia do cilindro maciço ao redor do seu centro de massa é
Substituindo a aceleração angular pela aceleração do centro de massa, naquela relação que eu falei no início desse Passo 2.
Agora que encontramos as trações de duas formas, é só iguala-las.
E finalmente, pra encontrar a tração, a gente substitui o valor da aceleração do centro de massa.
Passo 4
d)
Já encontramos né. A aceleração do centro de massa de um corpo que rola sem deslizar é a própria aceleração linear, afinal, o centro de massa não possui aceleração angular.
Resposta
b)
Apenas a força peso realiza trabalho.
c)
d)