P1 de Probabilidade e Estatística da PUCRIO - 2015.1

b) Considere a seguinte afirmação: Se e são dois eventos mutuamente exclusivos, então , indicando que a ocorrência do evento não traz informação sobre a probabilidade de ocorrência do evento . Esta afirmativa é verdadeira ou falsa?

c) Seja “” uma v.a. contínua. Defina o que é a sua função de distribuição de probabilidade acumulada, , e enumere as suas propriedades.

d) Uma variável aleatória é tal que e . Calcule e .

O receptor de um determinado equipamento de uma rede de telecomunicações recebe mensagens de instruções através de três possíveis transmissores diferentes. Estatísticas da rede mostram que 50% das mensagens recebidas são enviadas pelo transmissor 1, 40% pelo transmissor 2 e 10% pelo transmissor 3. Para fins de garantia de integridade das informações, o protocolo de comunicação exige que o receptor confirme o recebimento repetindo ao seu transmissor a mensagem recebida. Entretanto, a chance dos transmissores enviarem mensagens contendo erros nos bits que os identificam é de 1%, 3% e 6%, respectivamente. Com base nessas estatísticas, calcule:

1. A probabilidade de chegar uma mensagem no receptor com erro de identificação do remetente e, portanto, o receptor não ter certeza sobre qual transmissor ele deve responder.
2. Para cada um dos três transmissores, a probabilidade deste ter sido o remetente de uma mensagem que chegou no receptor com erro na identificação.

O pessoal de controle de qualidade afirma que os rolos de fita isolante apresentam, em média, uma emenda a cada 50 metros. Admitindo que a distribuição do número de emendas a cada 50 metros é modelado por uma Poisson, calcule as probabilidades:

1. De que não exista nenhuma emenda em um rolo de 125 metros.
2. De ocorrerem no máximo duas emendas em um rolo de 125 metros.
3. De ocorrer pelo menos uma emenda em um rolo de 100 metros.

Suponha uma variável aleatória contínua com densidade , com suporte no intervalor [0,2].

1. Ache a constante “” que faz ser uma densidade de probabilidade.
2. Encontre a função de distribuição de probabilidade acumulada de “”.
3. Calcule a média e a variância da distribuição de “”.

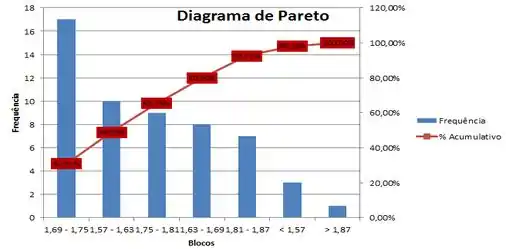
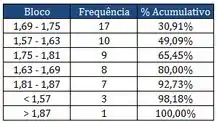
Os quadros abaixo, correspondem aos resultados das alturas dos alunos medidas em metros, matriculados em uma das turmas na matéria PROBEST 2013-2:

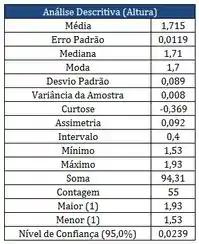
Dados Pareto:

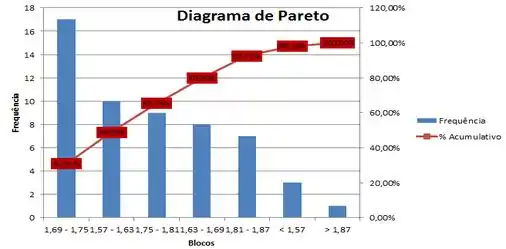
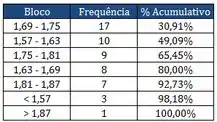
1. Através dos dados apresentados pelo Diagrama de Pareto, construa o Diagrama de frequência e o Histograma (Esboce Gráficos de Frequência e % Cumulativo).
2. Qual a quantidade de alunos com altura menor ou igual a 1,75?
3. Qual a quantidade de alunos com altura maior que 1,81?
4. Com relação à curtose, que tipo de curva podemos verificar? Por quê?
5. Quais são as medidas de Dispersão?
6. Se a probabilidade de um aluno de probest faltar a aula é de 5% e, suponha que os alunos faltem às aulas de maneira independente entre si e no tempo, qual a chance de, nessa turma, o professor não ter nenhum aluno presente em um determinado dia de aula?

Os quadros abaixo, correspondem aos resultados das alturas dos alunos medidas em metros, matriculados em uma das turmas na matéria PROBEST 2013-2:

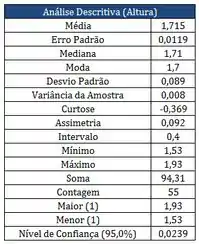
Dados Pareto:

1. Se a probabilidade de um aluno de probest faltar à aula é de 5% e suponde que os alunos faltem às aulas de maneira independente entre si e no tempo, qual a chance de, nessa turma, o professor não ter nenhum aluno presente em um determinado dia de aula?