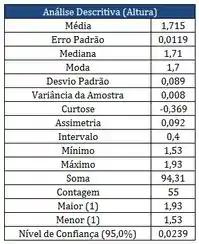
Os quadros abaixo, correspondem aos resultados das alturas dos alunos medidas em metros, matriculados em uma das turmas na matéria PROBEST 2013-2:
Dados Pareto:
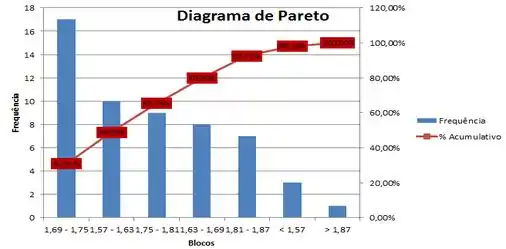
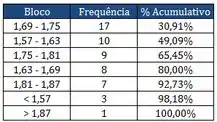
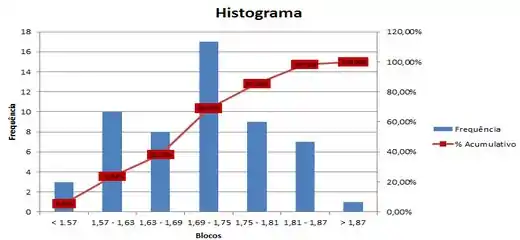
- Através dos dados apresentados pelo Diagrama de Pareto, construa o Diagrama de frequência e o Histograma (Esboce Gráficos de Frequência e % Cumulativo).
- Qual a quantidade de alunos com altura menor ou igual a 1,75?
- Qual a quantidade de alunos com altura maior que 1,81?
- Com relação à curtose, que tipo de curva podemos verificar? Por quê?
- Quais são as medidas de Dispersão?
- Se a probabilidade de um aluno de probest faltar a aula é de 5% e, suponha que os alunos faltem às aulas de maneira independente entre si e no tempo, qual a chance de, nessa turma, o professor não ter nenhum aluno presente em um determinado dia de aula?
Passo 1
(a)
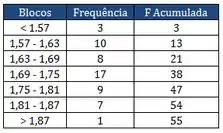
Pra construir o histograma preciso colocar os blocos em ordem crescente, do até o . Independente da frequência de cada um.
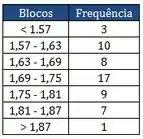
A gente pode anexar mais uma coluna nessa tabela, com as frequências acumulando.
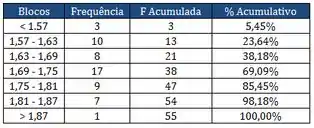
E com isso a gente pode fazer a porcentagem relativa acumulada, dividindo as frequências acumuladas pelo total que é
Passo 2
Agora é só fazer o histograma, representando tanto as frequências quanto as acumuladas.
Passo 3
(b)
Quantidade de alunos com altura menor ou igual a é só ir somando, ou pegar a frequência acumulada.
Passo 4
(c)
Quantidade de alunos com ou mais é só somar ali ... alunos.
Passo 5
(d)
Se você olhar ali na tabela de cima, o valor da curtose é . Curtose negativa significa falta de curtose, então temos uma curva leptocúrtica. Ela tem um formato mais pontudo, mais agudo no centro e é menos espalhada.
Passo 6
(e)
Algumas medidas de dispersão podem ser vistas na tabela:
E algumas a gente pode calcular..
E o coeficiente de variação:
Passo 7
(f)
O total de alunos é de e a probabilidade de algum faltar é de . Se é a v.a. que representa o nº de alunos que faltam aula.
Pra gente calcular a probabilidade do professor não ter aluno nenhum pra dar aula, temos que calcular , probabilidade dos alunos faltarem.
Só usar a função de probabilidade da Binomial.
Bem baixa essa probabilidade, alunos muito dedicados.
Resposta
Ei, a resposta está no passo a passo :)