Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Covariância e Correlação para V.a. Multidimensionais

Ver Teoria
Exercício 231234567891011121314151617181920212224

Enunciado

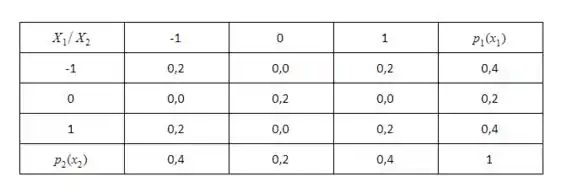
Sejam (X1, X2) a variável aleatória bidimensional cuja distribuição conjunta é dada pela tabela:

(a) Calcule E ( X i ) e v a r ( X i ) , sendo i = 1,2 .

(b) Calcule E ( X 1 ⋅ X 2 ) , C o v ( X 1 ,   X 2 ) e v a r ( X 1   −   X 2 ) . As v.a.‘s X 1 e X 2 são independentes?

(c) O que se pode dizer sobre a veracidade da afirmação: "Se X 1 e X 2 são independentes, então C o v ( X 1 ,   X 2 ) = 0 "? Justifique.

(d) O que se pode dizer com relação a esta afirmação: "Se C o v ( X 1 ,   X 2 ) = 0 , então X 1 e X 2 são independentes"? Justifique

Passo 1

(a) A última coluna da tabela nos dá a distribuição das probabilidades da v.a. X 1 . Para calcular E ( X 1 ) , basta multiplicar cada valor por sua probabilidade e somar:

E ( X 1 )   =   ( - 1 ) × 0,4   +   0 × 0,2   +   1 × 0,4 = 0

Mesma coisa para X 2 :

E ( X 2 )   =   ( - 1 ) × 0,4   +   0 × 0,2   +   1 × 0,4 = 0

Passo 2

Agora, observando que X 1 e X 2 têm a mesma distribuição de probabilidade, calcularemos a variância apenas de X 1 , pois a variancia de X 2 será igual. Vamos usar a fórmula da variância:

v a r ( X 1 )   =   E ( X 1 2 )   -   E ( X 1 ) 2 .

Passo 3

Como E ( X 1 )   =   0 , temos que E ( X 1 ) 2   =   0 .

Para calcular E ( X 1 2 ) ,   vamos ver a distribuição de probabilidades da v.a. X 1 2 :

Como X 1 só pode ser -1, 0 ou 1, temos que X 1 2 só pode assumir os valores 0 e 1.

P ( X 1 2 = 0 )   =   P ( X 1 = 0 ) = 0,2 ;

P ( X 1 2 = 1 )   =   P ( X 1 = 1   o u   X 1 = - 1 )   =   P ( X 1 = 1 )   +   P ( X 1 =   - 1 )   =   0,4   +   0,4   =   0,8 .

Assim, E ( X 1 2 )   =   0 × 0,2   +   1 × 0,8   =   0,8  

Passo 4

Voltando pra fórmula da variância:

v a r ( X 1 )   =   E ( X 1 2 )   -   E ( X 1 ) 2 = 0,8 - 0 = 0,8 .

Passo 5

(b) Para calcular E ( X 1 ⋅ X 2 ) , temos que encontrar a distribuição de probabilidades da v.a. X 1 ⋅ X 2 e depois calcular sua esperança:

  1. X 1 ⋅ X 2   =   - 1 se, e somente se: X 1 = 1   e   X 2 =   - 1 ou X 1 =   - 1   e   X 2 =   1
  2. X 1 ⋅ X 2 =   1 se, e somente se X 1 = 1   e   X 2 = 1 ou X 1 =   - 1   e   X 2 =   - 1
  3. X 1 ⋅ X 2 =   0   se, e somente se X 1 =   - 1   e   X 2 = 0 ou X 1 =   0   e   X 2 =   0 ou X 1 = 1   e   X 2 = 0 ou X 1 =   0   e   X 2 =   - 1   ou X 1 =   0   e   X 2 =   1  

Passo 6

Agora para descobrir as probabilidades, basta somar a de cada caso:

P ( X 1 ⋅ X 2   =   - 1 )   =   P ( X 1 = 1   e   X 2 =   - 1 ) + P ( X 1 =   - 1   e   X 2 =   1 ) = 0,2 + 0,2 = 0,4

P ( X 1 ⋅ X 2   =   1 )   =   P ( X 1 = 1   e   X 2 =   1 ) + P ( X 1 =   - 1   e   X 2 =   - 1 ) = 0,2 + 0,2 = 0,4

P ( X 1 ⋅ X 2 =   0 ) =   P ( X 1 =   - 1   e   X 2 = 0 ) + P ( X 1 =   0   e   X 2 =   0 )   +   …   +   P (   X 1 =   0   e   X 2 =   1 )  

→ P ( X 1 ⋅ X 2 =   0 )   =   0,2

Passo 7

Agora vamos calcular a esperança:

E ( X 1 ⋅ X 2 ) = ( - 1 ) × 0,4   +   1 × 0,4   +   0 × 0,2 = 0

Passo 8

Pra calcular a covariância, temos que lembrar da fórmula geral:

C o v ( X 1 , X 2 )   =   E ( X 1 ⋅ X 2 )   -   E ( X 1 ) ⋅ E ( X 2 )

No nosso caso:

C o v ( X 1 , X 2 )   = 0   -   0 × 0 = 0

Passo 9

Pra calcular v a r ( X 1 - X 2 ) , a fórmula é:

v a r ( X 1 - X 2 )   =   v a r ( X 1 ) + v a r ( X 2 )   -   2 ⋅ C o v ( X 1 , X 2 )   =   0,8 + 0,8   -   2 × 0   =   1,6 .

Passo 10

As variáveis não são independentes, pois P ( X 1 =   - 1 , X 2 =   - 1 )   =   0,2     que é diferente de

P ( X 1 =   - 1 ) × P ( X 2 =   - 1 )   =   ( 0,4 ) × ( 0,4 )

Passo 11

(c) A afirmação é verdadeira, pois se X   e   Y independentes, então E ( X ⋅ Y )   =   E ( X ) ⋅ E ( Y ) .

Substituindo na fórmula da covariância, temos que

C o v ( X , Y )   =   E ( X ⋅ Y )   -   E ( X ) ⋅ E ( Y )   = E ( X ) ⋅ E ( Y )   -   E ( X ) ⋅ E ( Y )   =   0 .  

Passo 12

(d) A afirmação é falsa. Um contra-exemplo são as próprias v.a’s do exercício.

Resposta

Resposta

Exercícios de Livros Relacionados

A variável aleatória X tem uma distribuição de probabilidades: f X ( x ) = x 8 ,0 ≤ x ≤ 4 Encontre a distribuição de probabilidades de Y=(X-2)^2
Mostre que se X 1 , X 2 , X 3 , . . . , X p forem variáveis aleatoriamente independentes e Y = c 1 X 1 + c 2 X 2 + c 3 X 3 + . . . + c p X p V ( Y ) = c 2 1 V ( X 1 ) + c 2 2 V ( X 2 ) + . . . + c 2 p
Considere a situação do Problema 10 do Capítulo 6. Verifique se E(XY) = E(X) E(Y). O que você pode concluir?
Considere a situação do Problema 10 do Capítulo 6. Verifique se X e Y são independentes.
Suponha que X tenha uma distribuição de probabilidades uniformes f X ( x ) = 1 ,1 ≤ x ≤ 2 Encontre a distribuição de probabilidades da variável aleatória Y=e^x