Determinar a primeira iteração para encontrar os autovalores da matriz com o método de Francis:
Com
Passo 1
Se:
Como , devemos zerar apenas o elemento . Assim para obtermos :
Zeramos o termo :
Onde:
A matriz das “letrinhas” e:
Passo 2
Se:
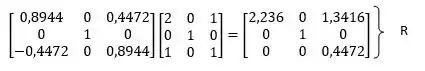
Agora temos que e então , e, portanto .
Com isso:
O termo da matriz triangular inferior
Isso significa que devemos fazer outra iteração.
Resposta
Exercícios de Livros Relacionados
Usando o método Q R , determinar todos os autovalores das matrizes: A = 4 4 - 3 0 8 1 0 2 - 1 ; B = 12 3 1 - 9 - 2 - 3 14 6 2 com precisão de 10 - 2 .
Usando o método QR, uma única vez, na matriz: A = 1 1 3 2 0 1 2 1 - 1 e possível estimar seus autovalores?
Determinar o autovalor de maior valor absoluto da matriz: A = 4 2 2 2 5 1 2 1 6 usando o método das potências. Use como vetor inicial y 0 =8 9 , 8 9 ,1 t . Dê seu valor aproximado após três iterações.
Considere a matrizes: A = 10 - 1 0 - 1 2 0 0 0 1 ; B = 100 0 99 0 20 0 99 0 101 Determine os autovalores de A, usando:a) Caso haja convergência pelo método de Rutishauser, o que se deve esperar?b) Det
Considere a matriz: A = 4 1 1 2 4 1 0 1 4 Determine os autovalores de A, com precisão de 10 - 2 , usando:a) o método L R ;b) o método Q R .