Opa, tenho uma boa notícia, não vamos precisar resolver o sistema no final! Ótimo né? Podemos parar nas equações. Show, vamos lá.
Temos o seguinte:
E teremos intervalos de modo que:
Então vai ficar assim:
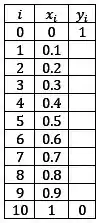
Beleza, agora vamos substituir as derivadas na nossa EDO:
Multiplicando os dois lados por :
Juntando os termos iguais:
:
:
:
:
:
:
:
:
:
