Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Métodos das Diferenças Finitas

Ver Teoria
Exercício 512346789

Enunciado

Resolva pelo método das Diferenças Finitas, o seguinte problema de valor de contorno com h = 0.2

y ' ' = 3 x y ' - y + x y 0 = 0 y ' 1 = 0

Passo 1

Temos o seguinte:

y ' ' = 3 x y ' - y + x

E teremos n intervalos de modo que:

n = b - a h = 1 0.2 = 5

Então vai ficar assim:

Ué, normalmente a gente tem o y n também né? Que nesse caso é o y 5 . Mas a condição de fronteira que ele deu pra gente foi: y ' 1 = 0 ⇔ y 5 ' = 0

Normalmente as duas condições são em y x e não em y ' x ! E agora?

Bom, por que não aproximarmos aquela derivada também? A gente aproxima todas as outras mesmo . . .

Só que como a ideia aqui é eliminar uma variável, teríamos que usar a diferença atrasada! Assim:

y i ' ≅ y i - y i - 1 h

y 5 ' = 0 ≅ y 5 - y 4 h

y 5 ≅ y 4

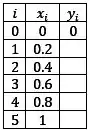
Agora podemos completar nossa tabela:

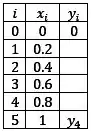
Passo 2

Beleza, agora vamos substituir as derivadas na nossa EDO:

y ' ' = 3 x y ' - y + x

y i + 1 - 2 y i + y i - 1 h 2 = 3 x i y i + 1 - y i - 1 2 h - y i + x i

Multiplicando os dois lados por h 2 :

y i + 1 - 2 y i + y i - 1 = 3 h 2 x i y i + 1 - y i - 1 - h 2 y i + h 2 x i

Juntando os termos iguais:

y i + 1 1 - 3 h 2 x i + y i - 2 + h 2 + y i - 1 1 + 3 h 2 x i = h 2 x i

1 - 0.3 x i y i + 1 - 1.96 y i + 1 + 0.3 x i y i - 1 = 0.04 x i

i = 1 :

1 - 0.3 x 1 y 2 - 1.96 y 1 + 1 + 0.3 x 1 y 0 = 0.04 x 1

0.94 y 2 - 1.96 y 1 = 0.008

i = 2 :

1 - 0.3 x 2 y 3 - 1.96 y 2 + 1 + 0.3 x 2 y 1 = 0.04 x 2

0.88 y 3 - 1.96 y 2 + 1.12 y 1 = 0.016

i = 3 :

1 - 0.3 x 3 y 4 - 1.96 y 3 + 1 + 0.3 x 3 y 2 = 0.04 x 3

0.82 y 4 - 1.96 y 3 + 1.18 y 2 = 0.0 24

i = 4 :

1 - 0.3 x 4 y 5 - 1.96 y 4 + 1 + 0.3 x 4 y 3 = 0.04 x 4

- 1.2 y 4 + 1.24 y 3 = 0.032

Passo 3

O sistema na forma matricial fica:

- 1.96 0.94 0 0 1.12 - 1.96 0.88 0 0 1.18 - 1.96 0.82 0 0 1.24 - 1.2 y 1 y 2 y 3 y 4 = 0.008 0.016 0.024 0.032

Fazendo a Eliminação de Gauss:

- 1.96 0.94 0 0 1.12 - 1.96 0.88 0 0 1.18 - 1.96 0.82 0 0 1.24 - 1.2 0.008 0.016 0.024 0.032 → L 2 ← L 2 + 0.57143 L 1 - 1.96 0.94 0 0 0 - 1.42286 0.88 0 0 1.18 - 1.96 0.82 0 0 1.24 - 1.2 0.008 0.02057 0.024 0.032 → L 3 ← L 3 + 0.82932 L 2 - 1.96 0.94 0 0 0 - 1.42286 0.88 0 0 0 - 1.23020 0.82 0 0 1.24 - 1.2 0.008 0.02057 0.04106 0.032 → L 4 ← L 4 + 1.00797 L 3 → L 3 ← L 3 + 0.82932 L 2 - 1.96 0.94 0 0 0 - 1.42286 0.88 0 0 0 - 1.23020 0.82 0 0 0 - 0.37347 0.008 0.02057 0.04106 0.07339

Retrosubstituindo:

y 1 = - 0.05977

y 2 = - 0.11611

y 3 = - 0.16436

y 4 = - 0.19650

y 5 = - 0.19650

Resposta

y 0.2 ≅ - 0.05977

y 0.4 ≅ - 0.11611

y 0.6 ≅ - 0.16436

y 0.8 ≅ - 0.19650

y 1 ≅ - 0.19650

Exercícios de Livros Relacionados

Uma parede, com 0,12m de espessura e difusividade térmica de 1,5×10 - 6m 2/ s , encontra-se inicialmente a uma temperatura uniforme igual a 85 ° C . Subitamente, uma de suas faces tem a sua temperatur
O critério de estabilidade para o método explícito exige que o coeficiente do termo T m p na equação de diferenças finitas unidimensional seja zero ou positivo. Analise a situação na qual as temperatu
Um fino bastão com diâmetro D está inicialmente em equilíbrio com a sua vizinhança, um grande recipiente, onde há vácuo, a uma temperatura T v i z . De repente, uma corrente elétrica I ( A ) é passada
Um cilindro sólido redondo, feito com um material plástico ( α=6 × 10 - 7 m 2 / s ) , está inicialmente a uma temperatura uniforme de 20 ° C e se encontra isolado ao longo de sua superfície lateral e
Seja o Problema 5.9, exceto pelo fato de que agora o volume combinado do banho de óleo e da esfera é igual a V=1m 3 . O banho de óleo é bem misturado e isolado termicamente. (a) Considerando que as pr