Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Métodos das Diferenças Finitas

Ver Teoria
Exercício 412356789

Enunciado

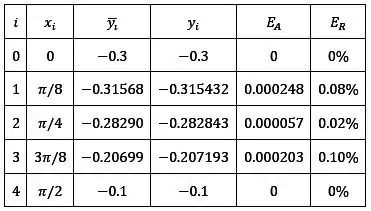
O PVC abaixo

y ' ' = y ' + 2 y + cos ⁡ x ,       0 ≤ x ≤ π 2 y 0 = - 0.3 y π 2 = - 0.1

tem como solução y = - 1 10 sin ⁡ x + 3 cos ⁡ x . Use o método das diferenças finitas para aproximar a solução e compare com a solução real para h = π 8

Passo 1

a Temos o seguinte:

y ' ' = y ' + 2 y + cos ⁡ x

E teremos n intervalos de modo que:

n = b - a h = π 2 π 8 = 4

Então vai ficar assim:

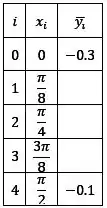
Beleza, agora vamos substituir as derivadas na nossa EDO:

y ' ' = y ' + 2 y + cos ⁡ x

y i + 1 - 2 y i + y i - 1 h 2 = y i + 1 - y i - 1 2 h + 2 y i + cos ⁡ x i

Multiplicando os dois lados por h 2 :

y i + 1 - 2 y i + y i - 1 = h 2 y i + 1 - y i - 1 + 2 h 2 y i + h 2 cos ⁡ x i

Juntando os termos iguais:

y i + 1 1 - h 2 + y i - 2 - 2 h 2 + y i - 1 1 + h 2 = h 2 cos ⁡ x i

0.80365 y i + 1 - 2.30843 y i + 1.19635 y i - 1 = 0.15421 cos ⁡ x i

i = 1 :

0.80365 y 2 - 2.30843 y 1 + 1.19635 y 0 = 0.15421 cos ⁡ x 1

0.80365 y 2 - 2.30843 y 1 = 0.501376

i = 2 :

0.80365 y 3 - 2.30843 y 2 + 1.19635 y 1 = 0.15421 cos ⁡ x 2

0.80365 y 3 - 2.30843 y 2 + 1.19635 y 1 = 0.109043

i = 3 :

0.80365 y 4 - 2.30843 y 3 + 1.19635 y 2 = 0.15421 cos ⁡ x 3

- 2.30843 y 3 + 1.19635 y 2 = 0.139379

Passo 2

O sistema na forma matricial fica:

- 2.30843 0.80365 0 1.19635 - 2.30843 0.80365 0 1.19635 - 2.30843 y 1 y 2 y 3 = 0.501376 0.109043 0.139379

Fazendo a Eliminação de Gauss:

- 2.30843 0.80365 0 1.19635 - 2.30843 0.80365 0 1.19635 - 2.30843 0.501376 0.109043 0.139379 → L 2 ← L 2 + 0.51825 L 1 - 2.30843 0.80365 0 0 - 1.89194 0.80365 0 1.19635 - 2.30843 0.501376 0.36888 0.139379 → L 3 ← L 3 + 0.63234 L 2 - 2.30843 0.80365 0 0 - 1.89194 0.80365 0 0 - 1.80025 0.501376 0.36888 0.37264

Retrosubstituindo:

y 1 = - 0.31568

y 2 = - 0.28290

y 3 = - 0.20699

Completando a tabelinha já com os valores exatos e com o erro ficamos com:

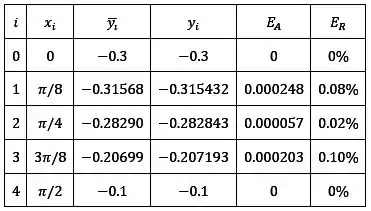
Resposta

Exercícios de Livros Relacionados

Uma parede, com 0,12m de espessura e difusividade térmica de 1,5×10 - 6m 2/ s , encontra-se inicialmente a uma temperatura uniforme igual a 85 ° C . Subitamente, uma de suas faces tem a sua temperatur
O critério de estabilidade para o método explícito exige que o coeficiente do termo T m p na equação de diferenças finitas unidimensional seja zero ou positivo. Analise a situação na qual as temperatu
Um fino bastão com diâmetro D está inicialmente em equilíbrio com a sua vizinhança, um grande recipiente, onde há vácuo, a uma temperatura T v i z . De repente, uma corrente elétrica I ( A ) é passada
Um cilindro sólido redondo, feito com um material plástico ( α=6 × 10 - 7 m 2 / s ) , está inicialmente a uma temperatura uniforme de 20 ° C e se encontra isolado ao longo de sua superfície lateral e
Seja o Problema 5.9, exceto pelo fato de que agora o volume combinado do banho de óleo e da esfera é igual a V=1m 3 . O banho de óleo é bem misturado e isolado termicamente. (a) Considerando que as pr