Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Métodos das Diferenças Finitas

Ver Teoria
Exercício 312456789

Enunciado

Resolva pelo método das diferenças finitas o PVC:

y ' ' x + 2 y ' x + y x = x y 0 = 0                                                                       y 1 = - 1                                                                

Considere h = 0.25

Passo 1

Fala, td blz? Bora resolver esse PVC? A primeira coisa é que você tem que estar afiado nas derivações numéricas, manjando do paranauê!!

A gente sabe o seguinte:

n = b - a h

n = 1 - 0 0.25 = 4

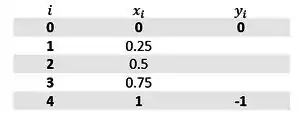
Então nossa tabelinha terá 4 intervalos, e por consequência 5 pontos, okay?

Passo 2

Agora bora substituir na EDO as derivadas numéricas

y ' ' x + 2 y ' x + y x = x

y i + 1 - 2 y i + y i - 1 h 2 + 2 y i + 1 - y i - 1 2 h + y i = x i

Multiplicando os dois lados por h 2

y i + 1 - 2 y i + y i - 1 + h y i + 1 - y i - 1 + h 2 y i = h 2 x i

E juntando os termos semelhantes, temos:

y i + 1 1 + h + y i - 2 + h 2 + y i - 1 1 - h = h 2 x i

Substituindo na fórmula o passo h = 0.25

1.25 y i + 1 - 1.9375 y i + 0.75 y i - 1 = 0.25 2 x i

Para i = 1 , teremos:

1.25 y 2 - 1.9375 y 1 + 0.75 y 0 = 0.25 2 x 1

1.25 y 2 - 1.9375 y 1 = 0.015625

Para i = 2 , teremos:

1.25 y 3 - 1.9375 y 2 + 0.75 y 1 = 0.25 2 x 2

1.25 y 3 - 1.9375 y 2 + 0.75 y 1 = 0.03125

Para i = 3 , teremos:

1.25 y 4 - 1.9375 y 3 + 0.75 y 2 = 0.25 2 x 3

Lá da tabela que nós montamos no passo 1 sabemos que y 4 = - 1 , podemos dar uma arrumadinha na terceira equação né?!

- 1.9375 y 3 + 0.75 y 2 = 1.296875

Se você reparar bem, caímos num sisteminha de 3 equações e 3 incógnitas. Basta acha-las e completar a tabela agora.

Passo 3

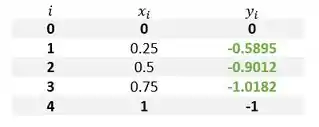
1.25 y 2 - 1.9375 y 1 = 0.015625 1.25 y 3 - 1.9375 y 2 + 0.75 y 1 = 0.03125 - 1.9375 y 3 + 0.75 y 2 = 1.296875

Resolvendo o sistemas:

y 3 = - 1.0182

y 2 = - 0.9012

y 1 = - 0.5895

Resposta

y 3 = - 1.0182

y 2 = - 0.9012

y 1 = - 0.5895

Exercícios de Livros Relacionados

Uma parede, com 0,12m de espessura e difusividade térmica de 1,5×10 - 6m 2/ s , encontra-se inicialmente a uma temperatura uniforme igual a 85 ° C . Subitamente, uma de suas faces tem a sua temperatur
O critério de estabilidade para o método explícito exige que o coeficiente do termo T m p na equação de diferenças finitas unidimensional seja zero ou positivo. Analise a situação na qual as temperatu
Um fino bastão com diâmetro D está inicialmente em equilíbrio com a sua vizinhança, um grande recipiente, onde há vácuo, a uma temperatura T v i z . De repente, uma corrente elétrica I ( A ) é passada
Um cilindro sólido redondo, feito com um material plástico ( α=6 × 10 - 7 m 2 / s ) , está inicialmente a uma temperatura uniforme de 20 ° C e se encontra isolado ao longo de sua superfície lateral e
Seja o Problema 5.9, exceto pelo fato de que agora o volume combinado do banho de óleo e da esfera é igual a V=1m 3 . O banho de óleo é bem misturado e isolado termicamente. (a) Considerando que as pr