Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Métodos das Diferenças Finitas

Ver Teoria
Exercício 123456789

Enunciado

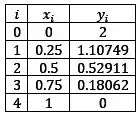
Resolva pelo método das diferenças finitas, o PVC:

y ' ' + 2 y ' + y = x y 0 = 2 y 1 = 0

usando h = 0.25

Passo 1

Temos o seguinte:

y ' ' + 2 y ' + y = x

E teremos n intervalos de modo que:

n = b - a h = 1 0.25 = 4

Então vai ficar assim:

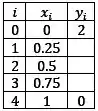
Beleza, agora vamos substituir as derivadas na nossa EDO:

y ' ' + 2 y ' + y = x

y i + 1 - 2 y i + y i - 1 h 2 + 2 y i + 1 - y i - 1 2 h + y i = x i

Multiplicando os dois lados por h 2 :

y i + 1 - 2 y i + y i - 1 + h y i + 1 - y i - 1 + h 2 y i = h 2 x i

Juntando os termos iguais:

y i + 1 1 + h + y i - 2 + h 2 + y i - 1 1 - h = h 2 x i

1.25 y i + 1 - 1.9375 y i + 0.75 y i - 1 = 0.25 2 x i

i = 1 :

1.25 y 2 - 1.9375 y 1 = - 1.484375

i = 2 :

1.25 y 3 - 1.9375 y 2 + 0.75 y 1 = 0 . 0 3125

i = 3 :

- 1.9375 y 3 + 0.75 y 2 = 0.046875

Então chegamos no sistema:

1.25 y 2 - 1.9375 y 1 = - 1.484375 1.25 y 3 - 1.9375 y 2 + 0.75 y 1 = 0 . 0 3125 - 1.9375 y 3 + 0.75 y 2 = 0.046875

Que passando para a forma matricial fica:

0 1.25 - 1.9375 1.25 - 1.9375 0.75 - 1.9375 0.75 0 y 3 y 2 y 1 = - 1.484375 0 . 0 3125 0.046875

Mais fácil que gravar aquela matriz genérica né?

Passo 2

Agora é só resolvermos o sistema:

0 1.25 - 1.9375 1.25 - 1.9375 0.75 - 1.9375 0.75 0 - 1.484375 0.03125 0.046875 → L 2 ⟷ L 1 1.25 - 1.9375 0.75 0 1.25 - 1.9375 - 1.9375 0.75 0 0.03125 - 1.484375 0.046875 → L 3 ← L 3 + 1.55 L 1 1.25 - 1.9375 0.75 0 1.25 - 1.9375 0 - 2.25313 1.16250 0.03125 - 1.484375 0.09531 → L 3 ← L 3 + 1.80250 L 2 1.25 - 1.9375 0.75 0 1.25 - 1.9375 0 0 - 2.32984 0.03125 - 1.484375 - 2.58027

Fazendo a retrosubstituição chegamos em:

y 1 = 1.10749

y 2 = 0.52911

y 3 = 0.18062

Completando nosso quadrinho:

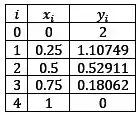
Resposta

Exercícios de Livros Relacionados

Uma parede, com 0,12m de espessura e difusividade térmica de 1,5×10 - 6m 2/ s , encontra-se inicialmente a uma temperatura uniforme igual a 85 ° C . Subitamente, uma de suas faces tem a sua temperatur
O critério de estabilidade para o método explícito exige que o coeficiente do termo T m p na equação de diferenças finitas unidimensional seja zero ou positivo. Analise a situação na qual as temperatu
Um fino bastão com diâmetro D está inicialmente em equilíbrio com a sua vizinhança, um grande recipiente, onde há vácuo, a uma temperatura T v i z . De repente, uma corrente elétrica I ( A ) é passada
Um cilindro sólido redondo, feito com um material plástico ( α=6 × 10 - 7 m 2 / s ) , está inicialmente a uma temperatura uniforme de 20 ° C e se encontra isolado ao longo de sua superfície lateral e
Seja o Problema 5.9, exceto pelo fato de que agora o volume combinado do banho de óleo e da esfera é igual a V=1m 3 . O banho de óleo é bem misturado e isolado termicamente. (a) Considerando que as pr