Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Métodos das Diferenças Finitas

Ver Teoria
Exercício 612345789

Enunciado

Formule, por diferenças finitas, sistemas de equações cuja solução aproxime a solução do seguinte PVC:

y ' ' = 2 y +   y 3 - t                                   y 0 = 4                                                                       y 4 = 2                                                                      

Considere, se necessário, h = 1 .

Passo 1

Faaaala aeee, o professor te deu um mole e pediu pra vc só montar o sistema de equações. Se vc olhar bem, existe um y 3 na EDO, que significa que o sistema que a gente vai obter é não linear. Ainda bem que ele nem quis que resolvesse e só achar e deixar lá. Então partiu!!

Já vamos fazer aquela tabelinha looouca pra ajudar a gente. Vamos precisar dela na hora de montar as equações pra cada i .

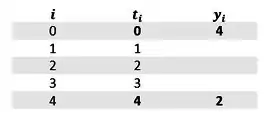
Bora substituir na EDO as derivadas numéricas.

y ' ' = y * s e n y + x   y

y i + 1 - 2 y i + y i - 1 h 2 =   2 y i +   y i 3 - t i  

Multiplicando os dois lados por h 2

y i + 1 - 2 y i + y i - 1 = 2 h 2 y i + h 2 y i 3 - h 2 t i  

E juntando os termos semelhantes, temos:

y i + 1 + y i - 2 - 2 h 2 - h 2 y i + y i - 1 = - h 2 t i

y i + 1 - y i 2 + h 2 ( 2 + y i 2 ) + y i - 1 = - h 2 t i

Como h = 1

y i + 1 - y i 2 + ( 2 + y i 2 ) + y i - 1 = - t i

Para i = 1 , teremos:

y 2 - y 1 2 + ( 2 + y 1 2 ) + y 0 = - t 1

Mas nós sabemos, direto das condições de contorno, que y 0 = 4 e t 1 = 1 . Então,

y 2 - y 1 4 + y 1 2 = - 5

Para i = 2 , teremos:

y 3 - y 2 2 + 2 + y 2 2 + y 1 = - t 2

y 3 - y 2 4 + y 2 2 + y 1 = - 2

Para i = 3 , teremos:

y 4 - y 3 2 + ( 2 + y 3 2 ) + y 2 = - t 3

Lá da tabela que nós montamos no passo 1 sabemos que y 4 = 2 e t 3 = 3 , então podemos substituir esse valores na equação.

- y 3 4 + y 3 2 ) + y 2 = - 5

Resposta

y 2 - y 1 4 + y 1 2 = - 5 y 3 - y 2 4 + y 2 2 + y 1 = - 2 - y 3 4 + y 3 2 ) + y 2 = - 5

Exercícios de Livros Relacionados

Uma parede, com 0,12m de espessura e difusividade térmica de 1,5×10 - 6m 2/ s , encontra-se inicialmente a uma temperatura uniforme igual a 85 ° C . Subitamente, uma de suas faces tem a sua temperatur
O critério de estabilidade para o método explícito exige que o coeficiente do termo T m p na equação de diferenças finitas unidimensional seja zero ou positivo. Analise a situação na qual as temperatu
Um fino bastão com diâmetro D está inicialmente em equilíbrio com a sua vizinhança, um grande recipiente, onde há vácuo, a uma temperatura T v i z . De repente, uma corrente elétrica I ( A ) é passada
Um cilindro sólido redondo, feito com um material plástico ( α=6 × 10 - 7 m 2 / s ) , está inicialmente a uma temperatura uniforme de 20 ° C e se encontra isolado ao longo de sua superfície lateral e
Seja o Problema 5.9, exceto pelo fato de que agora o volume combinado do banho de óleo e da esfera é igual a V=1m 3 . O banho de óleo é bem misturado e isolado termicamente. (a) Considerando que as pr