Calcular a EDO:
No intervalo , para e passo . Resolver pelo método de Runge-Kutta de 4ª ordem.
Passo 1
O primeiro passo nessas questões de EDO é sempre escrever as equações adaptadas ao problema do método que a gente tá usando. No caso do Runge-Kutta as equações são:

Começou a ficar meio feio né. Mas o que essas fórmulas aí querem dizer é o seguinte oh:
é tudo que tá do lado direito da igualdade okay? Então...
Para escrever a fórmula do , basta pegarmos e
- Onde tiver escrito , escreva ;
- Onde tiver escrito , escreva . E esse é o resultado da primeira equação e é o passo que o professor pediu.
A equação do fica assim então oh:
Beleza agora é só seguir a mesma idéia para as outras.
Em ao invés de usarmos , usaremos apenas .
Agora que já temos as equações adaptadas ao nosso problema vamos construir uma tabela pra facilitar nossa vida.
Passo 2
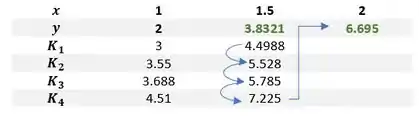
A tabela é essa aqui oh:

Nela vamos colocar os resultados de todos os cálculos blz? Por enquanto a linha do tá preenchida com os valores de 1 até 2 com passo 0.5 que foi o que o professor pediu no enunciado, lembra? Ele também disse que o , em outras palavras ele quer dizer que o primeiro valor de na tabela é 2.
Show de bolinhas, agora é só por a mão na massa e ir calculando todos os K para achar o próximo .
Coluna
Agora que já temos todos os valores de K, podemos calcular o valor de quando .
Passando tudo pra tabela temos:

Coluna .5
Agora que já temos todos os valores de K, podemos calcular o valor de quando .
Passando tudo pra tabela temos: