Um indivíduo está recebendo uma injeção intravenosa de glicose na taxa constante de . É um fato biológico que, dentro de certos limites, o corpo utiliza a glicose em uma taxa proporcional à sua concentração na corrente sanguínea. A EDO que modela esta situação é: , onde é o volume de sangue no corpo do indivíduo, consideraremos que a quantidade de glicose injetada não altera V apreciavelmente. A mudança da concentração de glicose no sangue é o resultado de dois fatores: um aumento devido à injeção intravenosa permanente e a redução devida à retirada da glicose sanguínea pelo corpo. Em um tempo t qualquer, a taxa de mudança de concentração devida à injeção intravenosa permanente é , e a taxa de mudança de concentração devida aos processos metabólicos é −𝑘𝑦, para alguma constante positiva. Supondo , e , como calcular, pelo método de Runge-Kutta de 4a. ordem, a concentração de glicose entre 10 e 14 minutos com 𝑦0 = 12.5 𝑒 ℎ = 1?
Passo 1
Antes de mais nada, bora substituir os valores que ele deu no enunciado diretinho na EDO.
Depois disso, SEEMPRE nessas questões de EDO precisamos escrever as equações adaptadas ao problema do método que a gente tá usando. No caso do Runge-Kutta as equações são:

Loucura, Loucura, Loucura. Maaaas vamos decifrar isso aí. O que essas fórmulas aí querem dizer é o seguinte oh:
é tudo que tá do lado direito da igualdade okay? Então...
Para escrever a fórmula do , basta pegarmos e
- Onde tiver escrito , escreva . Esse é o resultado da primeira equação e é o passo que o professor pediu.
A equação do fica assim então oh:
Beleza agora é só seguir a mesma idéia para as outras.
Em ao invés de usarmos , usaremos apenas .
Agora que já temos as equações adaptadas ao nosso problema vamos construir uma tabela pra facilitar nossa vida.
Passo 2
A tabela é essa aqui oh:

Nela vamos colocar os resultados de todos os cálculos blz? Por enquanto a linha do tá preenchida com os valores de 10 até 14 minutos e passo 1 que foi o que o professor pediu no enunciado, tranquilo até aqui? Ele também disse que . Em outras palavras ele quer dizer que quando .
Show de bolinhas, agora é só por a mão na massa e ir calculando todos os K para achar o próximo .
Coluna
Agora que já temos todos os valores de K, podemos calcular o valor de quando .
Passando tudo pra tabela temos:

Bora agora calcular os valores de K para a coluna .
Só substituir na fórmula do agora.
Passando tudo pra tabela temos:

Coluna
Agora que já temos todos os valores de K, podemos calcular o valor de quando .
Passando tudo pra tabela temos:
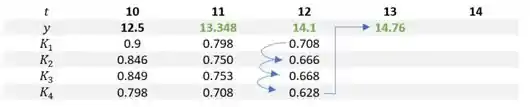
Agora temos que achar os valores de K para a coluna .
Agora que já temos todos os valores de K, podemos calcular o valor de quando .
Passando tudo pra tabela temos:
