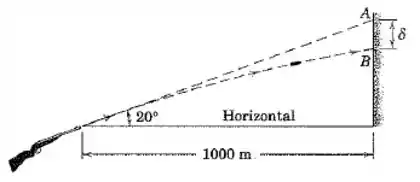
Se o cano da espingarda mostrada aponta para o ponto , calcule a distância abaixo de até o ponto onde a bala incide. A velocidade de saída no disparo da bala é de .
Passo 1
Para resolver essa questão, precisamos utilizar a fórmula do lançamento horizontal. Como o que interessa para nós é a altura, vamos usar a fórmula da altura do projétil.
O tempo, nós podemos pegar da fórmula da velocidade horizontal do projétil:
Logo:
Substituindo na fórmula da parcela vertical:
Além disso, precisamos lembrar que:
Substituindo na nossa fórmula:
Ou seja:
Passo 2
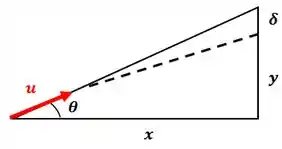
Pelo triângulo acima, podemos dizer que:
Passo 3
Então, vamos pegar a nossa fórmula para que encontramos no passo e adicionar dos dois lados da igualdade:
Substituindo os valores do enunciado: