02) Tomando como base a figura a seguir, pede-se:
a) Localize o CIVN da barra BC;
b) Calcule a velocidade angular da barra BC;
c) Calcule a velocidade do ponto C;
d) Calcule a velocidade angular da barra CD;
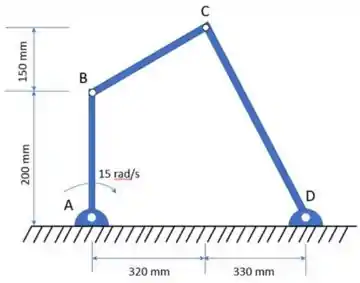
Passo 1
Eaí genteee, bora matar mais uma questão!
a) Esse exercício pede, primeiramente, para calcular o CIVN (Centro instantâneo de velocidade nula) da barra BC.
O CIVN fica localizado em um ponto que, no instante considerado, sua velocidade é nula. O interessante é que esse ponto não precisa, necessariamente, estar localizado dentro da barra.
Ele fica na intersecção de duas retas perpendiculares às velocidades de dois pontos.

Tipo assim, pra barra BC, por exemplo, se a gente encontrar as direções das velocidades nos pontos B e C, basta traçarmos retas perpendiculares a esses pontos e anotar a intersecção delas, esse será o CIVN da barra BC.
Vai ser exatamente essa a estratégia que vamos usar!
Começando pela velocidade do ponto B:
Se analisarmos a barra AB, o ponto A é um ponto fixo, então sua velocidade é nula em qualquer instante. Logo, A é o CIVN da barra AB. Consequentemente, vale que:
Show! Por esse produto vetorial, sabemos que a velocidade de B é perpendicular à barra AB. Vamos guardar isso, ok?
Olhando agora para a barra CD, temos também que D é um ponto fixo, logo ele possui velocidade nula e é o CIVN da barra CD. Então, vale que:
Logo, a velocidade em C é perpendicular à barra CD.
Mas, pensa comigo pessoal, as duas retas perpendiculares às velocidades de B e C são, respectivamente, AB e CD. Então, é só a gente encontrar o ponto de intersecção delas, e esse será o CIVN.
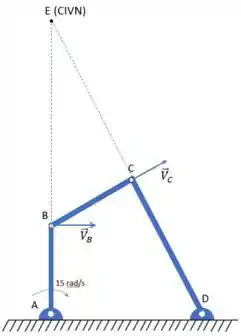
Prontinho! O ponto E é o CIVN da barra BC. Conseguiram entender bem?
Bora pra próxima!
Passo 2
b) Aqui precisamos calcular a velocidade angular da barra BC. Como já sabemos o CIVN dessa barra, podemos usar a seguinte equação:
Mas, quem que é ? Bora usar a equação do CIVN da barra AB, daí vem:
Onde rad/s.
Igualando as duas equações, chegamos que:
Massa! Para descobrir a velocidade angular de BC só nos falta saber o valor de . Vamos considerar os seguintes triângulos:
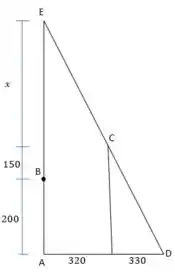
Daí vem:
Muito bom! Então
Voltando à nossa expressão para , temos:
Prontinho, matamos a letra B 😊
Passo 3
c) Devemos calcular a velocidade do ponto C. Para fazer isso, também podemos usar a equação relacionada ao CIVN da barra BC, ou seja:
Para encontrar podemos usar o teorema de Pitágoras:
Muito bom! Agora é só substituir na expressão para :
Ou:
Passo 4
d) Beleza gente, bora lá pra última letra. E, pra todo mundo ver como é importante notar os pontos que são CIVN, como D é CIVN da barra CD, podemos escrever como:
Também podemos achar por Pitágoras. Daí:
Massa! Mas, no item C, nós já descobrimos . Então, isolando vamos ter:
Obaa, finalmente terminamos essa questão. Bora ficar atento aos CIVN galera!!
Até a próxima 😉
Resposta
a) Resolução no texto
b)
c)
d)