Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Movimento curvilíneo

Ver Teoria
Exercício 10123456789

Enunciado

UFRJ, Mecânica 1, 2020.2, PF, Q3

No mecanismo ilustrado na figura o ponto C se movimenta ao longo de uma guia deslizante. No instante representado a velocidade do ponto C é igual a 2,0   m / s e está sendo reduzida à taxa de 8   m / s a cada segundo.

Para o instante representado na figura pede-se:

  1. Com um desenho do mecanismo, mostrar a localização do centro instantâneo de velocidade nula da caixa conectada nos pontos B e C.
  2. A magnitude da velocidade angular da barra A B é igual a?
  3. Em outro desenho, mostrar as componentes dos vetores aceleração dos pontos B e C.
  4. A magnitude da aceleração angular da barra AB é igual a?

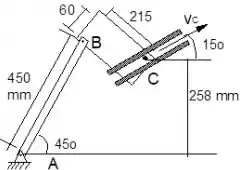
Passo 1

Faaaala, pessoal! Veja que o ponto C permanece em equilíbrio na direção perpendicular à guia, apresentando velocidade e aceleração só na direção paralela à guia. Enquanto isso, o ponto B se move circularmente em torno de A . Com isso em mente, seja O o centro instantâneo de velocidade da caixa conectada nos pontos B e C. Veja que O é determinado pelo encontro das retas perpendiculares às velocidades de B e C

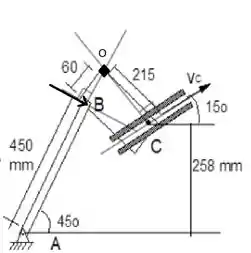
A ideia nessa questão é determinar a velocidade e aceleração angular em torno de O a partir das informações de C, para então determinar a velocidade e aceleração do ponto B.

Passo 2

Nesse pique, o que temos de determinar são às distâncias l 1 e l 2 dos pontos C e B , respectivamente a esse centro O . Da figura abaixo:

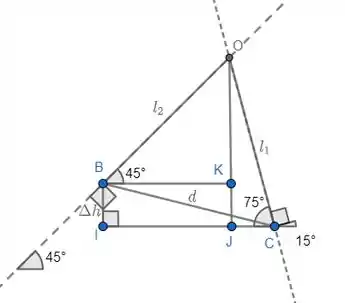
Temos:

  • Δ h : diferença de altura entre B e C
  • d : diagonal B C da caixa

Donde:

Δ h = h B - h C = 450 m m ⋅ sin ⁡ 45 ∘ - 258   m m = 60,198   m m

E ainda, por Pitágoras:

d = 60 2 + 215 2 = 223,215   m m

Com isso, para l 1 e l 2 :

D i r e ç ã o   x :                     l 1 cos ⁡ 75 ∘ + l 2 cos ⁡ 45 ∘ = d 2 - Δ h 2

D i r e ç ã o   y :                           l 1 sin ⁡ 75 ∘ - l 2 sin ⁡ 45 ∘ = Δ h                            

Assim, o sistema equivale a:

cos ⁡ 75 ∘ cos ⁡ 4 5 ∘ sin ⁡ 75 ∘ - sin ⁡ 4 5 ∘ l 1 l 2 = 214,944 60,198

Resolvendo por Crammer esse sistema, temos:

l 1 = 214,944 cos ⁡ 45 ∘ 60,198 - sin ⁡ 45 ∘ cos ⁡ 75 ∘ cos ⁡ 45 ∘ sin ⁡ 75 ∘ - sin ⁡ 45 ∘ =

= - 214,944 sin ⁡ 45 ∘ - 60,198 cos ⁡ 45 ∘ - cos ⁡ 75 ∘ sin ⁡ 45 ∘ - cos ⁡ 4 5 ∘ sin ⁡ 7 5 ∘ =

= 194,555 sin ⁡ 75 ∘ + 45 ∘ = 224,653   m m

Analogamente,

l 2 = cos ⁡ 75 ∘ 214,944 sin ⁡ 75 ∘ 60,198 cos ⁡ 75 ∘ cos ⁡ 45 ∘ sin ⁡ 75 ∘ - sin ⁡ 45 ∘ =

= 60,198 cos ⁡ 7 5 ∘ - 214,944 sin ⁡ 7 5 ∘ - cos ⁡ 75 ∘ sin ⁡ 45 ∘ - cos ⁡ 45 ∘ sin ⁡ 75 ∘

= - 192,040 - sin ⁡ 75 ∘ + 45 ∘ = 221,748   m m

Passo 3

Considerando o centro instantâneo de rotação O e a rotação de velocidade angular ω e aceleração angular α , temos:

ω = v C l 1 = v B l 2 ⇒ v B = v C l 2 l 1

α = a C l 1 = a B l 2 ⇒ a B = a C ⋅ l 2 l 1

Como l 2 l 1 = 221,748 224,653 = 0,987 , temos:

v B = 2,0 ⋅ 0,987 = 1,974   m / s

a B = - 8 m s 2 ⋅ 0,987 = - 7,896   m / s 2  

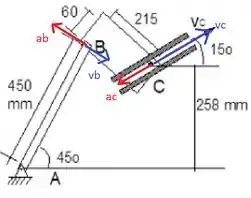
Passo 4

Assim, a velocidade e aceleração angular da barra AB é dada por:

ω A B = v B A B ¯ = 1,974   m / s 0,450 m = 4,387 r a d s     ( s e n t i d o   h o r á r i o )

α A B = a B A B ¯ = 7,896   m / s 0,450 m = 17,547 r a d s 2       ( s e n t i d o   a n t i - h o r á r i o )

Resposta

ω A B = 4,387 r a d s     ( s e n t i d o   h o r á r i o )

α A B = 17,547 r a d s 2       ( s e n t i d o   a n t i - h o r á r i o )

Exercícios de Livros Relacionados

O carro B faz uma curva de tal maneira que sua velocidade escalar é aumentada na razão de a t B = 0,5 e tm / s 2 , onde t é dado em segundos. Se um carro parte do repouso quando θ = 0 ° , determine as
Quando x = 3m , o caixote tem uma velocidade escalar de 6m / s que está aumentando a 1,8m / s 2 . Determine a direção da velocidade do caixote e a intensidade da aceleração do caixote nesse instante.
Elétrons são emitidos em A com uma velocidade u no ângulo θ para o espaço entre duas placas carregadas. O campo elétrico entre as placas é na direção E e repele os elétrons que se aproximam da placa s
Um cubo sólido de densidade uniforme e lados com dimensão b se encontra em equilíbrio na parte superior de um cilindro de raio R (Figura 2.C). Os planos dos quatro lados do cubo são paralelos ao eixo
Uma abóbora de massa 5 kg, lançada de um "canhão" feito por um aluno sob pressão atmosférica, em um ângulo de elevação de 45⁰, caiu a uma distância de 142 m do canhão. Os alunos utilizaram feixes de l