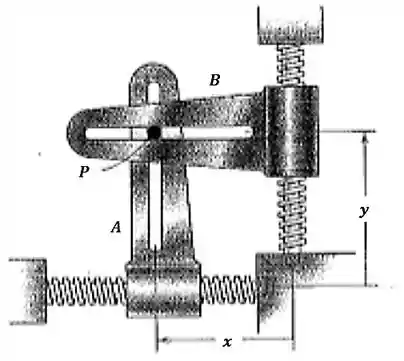
Os movimentos e das guias e com ranhuras em ângulo reto controlam o movimento curvilíneo do pino de conexão, que desliza nas duas ranhuras. Por um curto intervalo de tempo, os movimentos são regidos por , onde e são em milímetros e é em segundos. Calcule o módulo da velocidade e aceleração do pino para . Desenhe a direção da trajetória e indique a sua curvatura para esse instante.
Passo 1
O vetor deslocamento é dado por:
Sabendo que a velocidade é a derivada da posição no tempo, temos que:
E a aceleração é a derivada da velocidade com relação ao tempo:
Passo 2
Para , vamos ter que a velocidade será de:
E a aceleração vai ser igual a:
Passo 3
Com isso, podemos calcular o módulo da velocidade:
E:
Passo 4
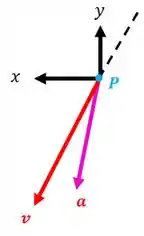
Então, o nosso desenho vai ficar assim: