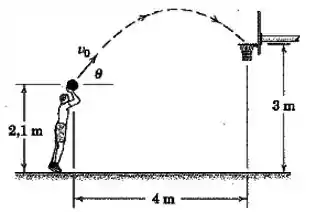
O jogador de basquete gosta de arremessar seu lance livre em um ângulo com a horizontal como mostrado. Que velocidade inicial fará com que a bola passe através do centro do aro?
Passo 1
Nós não sabemos quanto vale . Então vamos escrever tudo em função de . Assim, a componente do movimento será:
Sendo
Vamos calcular agora o tempo que o móvel leva pra alcançar a distância horizontal de
Guarde esse tempo, pois esse é o tempo que a bola leva voando.
Passo 2
Agora vamos usar o deslocamento vertical. A bola sai da coordenada e atinge a coordenada
Assim, podemos dizer que:
Para o tempo
Organizando:
Passo 3
Assim: