03) De acordo com a figura, o disco de raio e centro A rola sem escorregar com velocidade angular e aceleração angular sobre a pista interna do aro fixo de centro O e raio . Adotando a base ligada à barra OA, pede-se:
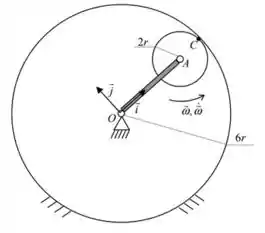
a) Determinar a velocidade e a aceleração angulares da haste OA;
b) Determinar a velocidade e a aceleração do ponto C do disco de centro A;
c) Esboçar um trecho da trajetória descrita pelo ponto C do disco de centro A;
d) Responder (justificando) se é possível ou não definir o triedro de Frenet para os pontos da trajetória esboçada no item anterior correspondentes ao contato do ponto C com a pista interna de aro de centro O.
Passo 1
Eaí gente bonita, tudo bom com vocês?
a) Pra começar bem nossa questão, precisamos determinar a velocidade e a aceleração angulares da haste OA.
Para fazer isso é uma ideia-chave determinar os centros instantâneos de rotação(CIR). Então, como o disco rola sem deslizar, temos . Logo, C é CIR do disco. Assim, podemos escrever que:
Por outro lado, o ponto O é fixo então . Assim, O é um CIR para a hasta OA. Daí, também podemos escrever que:
Beleza, agora é só igualar as duas expressões e teremos a velocidade angular da haste OA.
Logo, como:
Boa!! A primeira já foi 😊
Passo 2
b) Aqui precisamos determinar a velocidade e aceleração absolutas do ponto C.
Como já foi falado no item A, o ponto C é um CIR. Logo:
Já quanto à aceleração de C, pelo movimento plano geral, podemos dizer que:
O problema é que ainda não conhecemos . Então, bora repetir a mesma ideia para A:
Como O é um ponto fixo, . Daí:
Show, substituindo esse resultado em vem que:
Prontinho 😊
Passo 3
c) Nesse item devemos esboçar a trajetória do ponto C do disco.
Aqui é bem importante a gente guardar essa informação:
Sempre que temos um movimento de uma circunferência no interior de outra (disco dentro do aro), em que o movimento ocorre sem deslizamento temos que a curva da trajetória do ponto mais externo do disco é um hipociclóide.
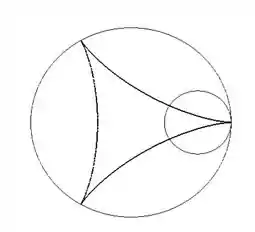
Essa curva tem o formato acima. Para desenhá-la precisamos identificar a relação entre o raio da circunferência interna e externa. Nesse caso, temos:
Logo:
Logo, a trajetória de C deve apresentar 3 pontos singulares, tipo bicos mesmo (igual a gente desenhou na figura acima), que apresentam em seu entorno singularidades chamadas de cúspides.
Passo 4
d) Devemos verificar se é possível, ou não, definir o triedro de Frenet para a trajetória do ponto C descrita no item anterior.
O triedro de Frenet é um conjunto de três versores, . Onde é o versor tangente e o versor normal, ambos a um ponto da trajetória, e é o chamado versor binomial.
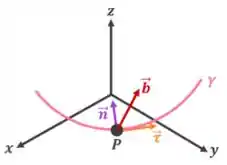
Para a nossa trajetória definida no item c, vemos que há três pontos singulares, nos quais não existe versor tangente . Sendo assim, não é possível definir um Triedro de Frenet, pois precisaria ser válido para todos os pontos da trajetória do ponto C, o que não ocorre.
Aee, terminamos! Valeu pela atenção pessoal, até a próxima!
Resposta
a)
b)
c) Resolução no texto.
d) Resolução no texto.