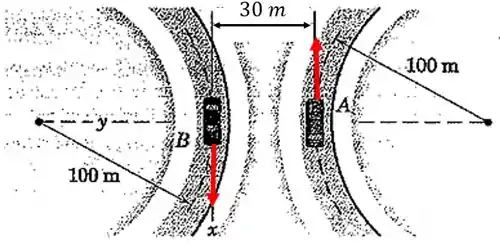
Os carros e estão contornando as curvas com velocidades iguais de . Determine a velocidade que parece ter para um observador se deslocando e girando com o carro para o instante representado. A curvatura da estrada para o carro afeta o resultado? Os eixos estão fixos no carro .
Passo 1
Quando temos o movimento relativo de corpos que realizam movimento de rotação e translação ao mesmo tempo, vamos usar a seguinte equação:
O que queremos determinar é a velocidade que parece ter para um observador se deslocando e girando com o carro , ou seja, queremos calcular a velocidade relativa .
O próximo passo é identificar quem está realizando o movimento relativo. Neste caso, é o carro , já que o eixo está fixo no carro . Então, a velocidade corresponde a velocidade absoluta do carro :
Vamos passar esta velocidade para :
Repare que o carro se move no sentido positivo do eixo , então o vetor velocidade é:
Como a velocidade do carro é igual a velocidade do carro , então:
Porém, o carro se move no sentido positivo do eixo :
A velocidade angular pode ser calculada, já que ambos os carros realizam movimento circular. Mas repare que a velocidade angular a ser calculada é a do carro (onde está o eixo fixo):
A velocidade angular é positiva, porque devido a posição dos eixos , o sentido positivo do eixo é apontando para dentro da tela.
E o vetor posição é a distância do carro até o eixo que está fixo em :
Passo 2
Agora que definimos o que é cada coisa da nossa equação, vamos substituir:
Vamos resolver o produto vetorial:
Então:
Passo 3
A questão quer saber se ao mudar o raio de curvatura do carro vai alterar a velocidade relativa. A resposta é não, porque usamos o raio de curvatura para calcular a velocidade angular . Mas sempre calculamos a velocidade angular do corpo onde está o eixo fixo e não no corpo em que estamos analisando o movimento relativo.