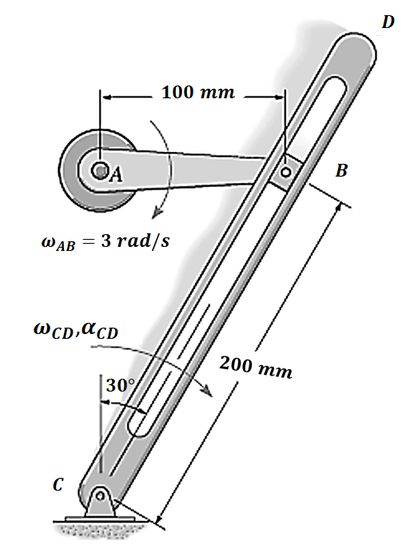
O bloco do mecanismo tem de ser deslocar na ranhura da barra . Se está se movendo a uma taxa constante , determine a velocidade angular e a aceleração angular da barra , na situação mostrada na figura.
Passo 1
Nesse tipo de questão, a primeira coisa que temos que fazer é posicionar o eixo que será móvel e aquele que será fixo.
Repare que o bloco se move ao longo da barra , então vamos posicionar o nosso eixo móvel () nesta barra onde ocorre o movimento:
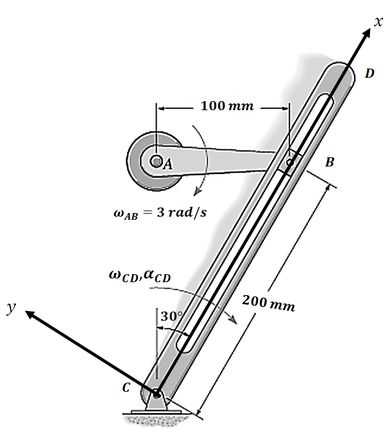
Nosso eixo fixo () vai ser aquele que estamos acostumados:
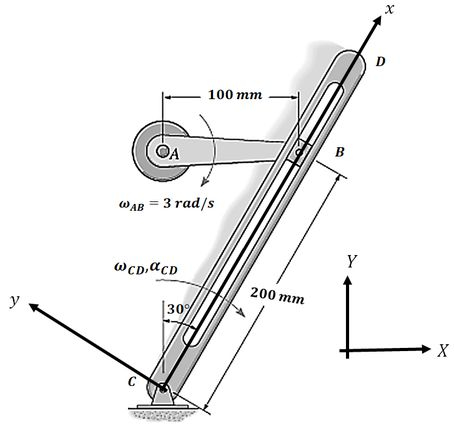
Passo 2
Feito isso podemos começar a resolver nossa questão. Vamos começar pela barra que temos alguma informação sobre o seu movimento que é a barra . Repare que nesta barra o ponto gira em torno do ponto que é fixo, então vamos usar nossa velha conhecida equação:
A velocidade angular da barra foi dada e como está girando no sentido horário é negativa:
O vetor posição de com relação ao ponto é:
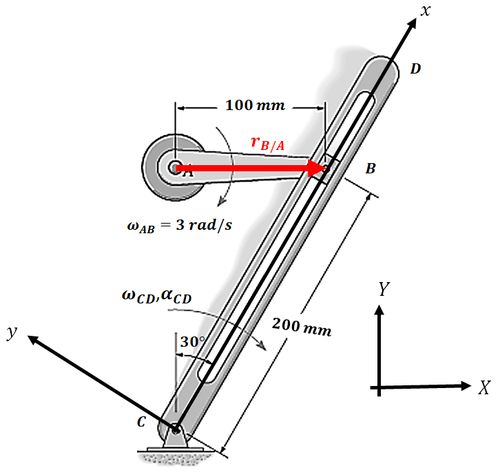
Agora é só fazermos o produto vetorial:
Passo 3
Nosso próximo passo é analisar a barra que é justamente a barra que a questão quer saber. Como nesta barra está o nosso eixo móvel, temos que usar a equação para eixos girantes:
Primeiro temos que identificar o que é cada termo da nossa equação com relação ao questão que queremos resolver!
A velocidade é a velocidade do ponto com relação ao referencial fixo. Mas repare que o ponto não se move ao longo do eixo, ele é fixo, logo sua velocidade é nula:
A velocidade angular que aparece na nossa equação é justamente o que a questão pede para determinamos. Repare que na figura que foi dada no enunciado já tem um sentido para a velocidade angular desta barra, então vamos só colocar o sentido que é negativo:
E o vetor ?
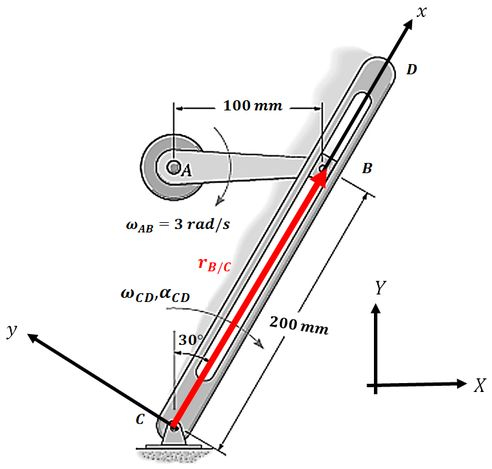
A velocidade relativa corresponde a velocidade que ponto tem quando ele se movimenta ao longo do eixo móvel. Como o ponto só pode se mover ao longo da barra , o vetor velocidade será:
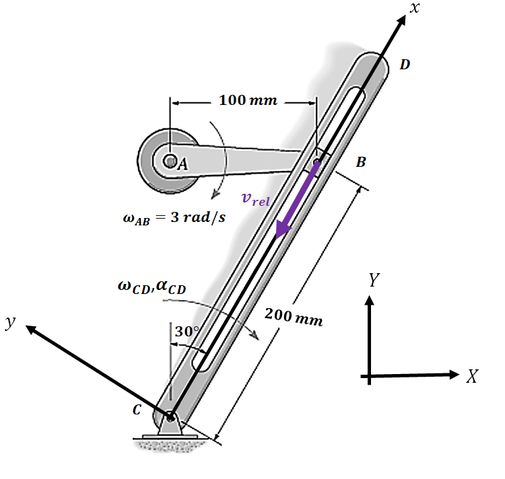
Repare que a velocidade está apontando para baixo, porque a barra está girando no sentido horário o que faz o ponto se mova para baixo ao longo do eixo móvel.

Porém, antes de colocar na nossa equação temos que decompor o vetor velocidade relativa para o eixo fixo . Como não sabemos seu valor, vamos ter que:
Agora sim podemos substituir tudo que achamos na nossa equação:
Vamos resolver este produto vetorial:
Então, temos que:
Passo 4
Lembra que já achamos a velocidade do ponto antes:
Então, vamos substituir esse valor nessa equação que achamos:
Agora temos que separar as componentes e em duas equações:
Da primeira equação temos que:
Substituindo isso na segunda equação:
O resultado ter dado positivo indica que arbitramos o sentido correto para o vetor (graças a dica da figura hahaha). Então, temos que:
E a velocidade relativa será:
Passo 5
Agora vamos analisar a aceleração do ponto . Primeiro vamos usar a barra que é a barra que temos alguma informação sobre seu movimento. Repare que o ponto faz um movimento circular em torno do ponto que é fixo, então:
Foi dito no enunciado da questão que a barra se move a uma taxa constante, portanto sua aceleração angular é nula:
Então nos sobra:
E já sabemos que:
E:
Substituindo isso na nossa equação, temos que:
Passo 6
Mas não é a aceleração do ponto que a questão pede. O que queremos é a aceleração angular da barra . Então, vamos analisar o movimento nesta barra sabendo que é nela que está nosso eixo móvel.
A equação da aceleração com relação ao eixo móvel é:
Vamos mais uma vez relacionar cada termo da equação com o que está acontecendo na situação do nosso problema.
Como o ponto está fixo, ele não possui aceleração:
A aceleração angular da barra nós não sabemos, mas pela figura é possível ver que o seu sentido é horário:
A aceleração relativa corresponde a aceleração do ponto quando ele se move no eixo móvel. Como o ponto só pode se mover ao longo da barra , o vetor aceleração relativa será:
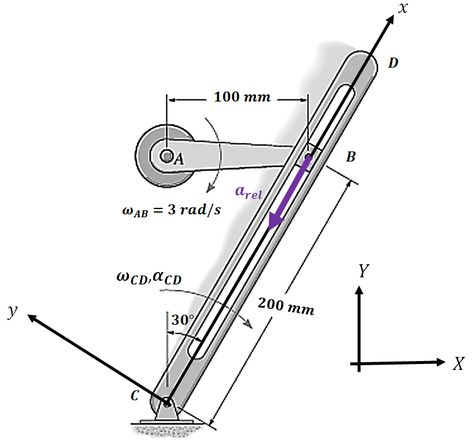
Precisamos decompor o vetor no eixo fixo :
Não esqueça que tem que decompor o vetor velocidade relativa (), cujo valor achamos no passo anterior, nos eixos também. Vai ficar assim:
E o restante dos termos nós já sabemos, então a nossa equação fica:
Vamos resolver cada um dos produtos vetoriais:
O próximo nós já tínhamos resolvido antes:
Então:
Vamos para o nosso último produto vetorial:
Agora, vamos substituir isso na nossa equação lá de cima:
Vamos dar aquela ajeitada na nossa equação:
Passo 7
Lembra que achamos um valor para a aceleração do ponto ?
Então, vamos substituir este valor na nossa equação:
Agora vamos separar as componentes e cada qual na sua equação:
Da segunda equação tiramos que:
Substituindo isso na primeira equação temos que:
Como o sinal deu negativo, significa que arbitramos o sentido contrário para a aceleração angular da barra . Como tínhamos arbitrado o sentido negativo, ela vai ser positiva: