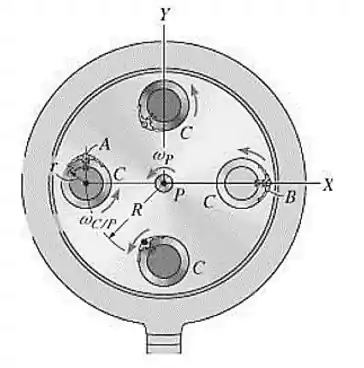
Um brinquedo de um parque de diversões consiste em uma plataforma girante , que tem velocidade angular constante , e quatro barquinhas, , montadas na plataforma, que têm velocidade angular constante , medida relativamente à plataforma. Determine a velocidade e a aceleração do passageiro , na situação mostrada na figura.
Dados: ; .
Passo 1
Vamos começar calculando a velocidade do passageiro que está no ponto :
Primeiro temos que identificar o que é cada termo da nossa equação no problema que queremos resolver!
A velocidade é aquela velocidade que queremos saber, então ela corresponde a velocidade do passageiro que está no ponto . Então, para ficar mais intuitivo:
A velocidade é a velocidade de onde está o nosso referencial fixo, que é o próprio brinquedo (é onde tudo está acontecendo):
Mas repare que a plataforma só gira em torno do ponto , ou seja, ela só tem velocidade angular:
A velocidade angular que aparece na nossa equação também é a do brinquedo que está girando com no sentido anti-horário (positivo), então o vetor será:
O vetor posição pode ser obtido na figura:
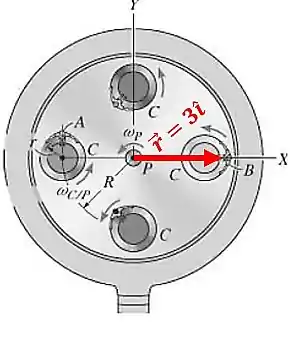
Como o raio do movimento da cadeiras é de , então o vetor será:
O vetor velocidade relativa corresponde a velocidade que o passageiro tem com relação ao brinquedo. Mas repare que só temos a velocidade angular relativa:
Como a cadeira está girando no sentido anti-horário, essa velocidade angular é positiva e seu vetor é:
Passo 2
Mas como vamos achar o valor da velocidade relativa ()? Repare que se olharmos só para as cadeiras, vamos ver que elas estão fazendo um movimento circular e também transladando devido a rotação da plataforma do brinquedo.
Sabemos que:
Porém, a velocidade angular da cadeira vai ser a soma da velocidade angular relativa (que a cadeira tem com relação à plataforma do brinquedo) com a velocidade angular do próprio brinquedo:
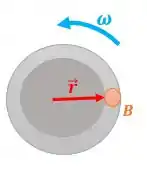
O vetor posição do passageiro com relação ao centro da cadeira é:
Então:
Nossa matriz fica:
Passo 3
Agora sim podemos calcular a velocidade do passageiro:
Vamos resolver o produto vetorial primeiro:
Então:
Passo 4
Agora vamos calcular a aceleração do passageiro:
Vamos mais uma vez relacionar cada termo da equação com o que está acontecendo na situação do problema.
A aceleração corresponde a aceleração do passageiro e justamente o que queremos saber:
A aceleração angular do brinquedo , neste nosso caso, é nula. Isso porque no enunciado foi dito que a plataforma do brinquedo tem uma velocidade angular constante.
A velocidade angular continua a mesma da outra equação:
A velocidade relativa também continua a mesma:
E a aceleração relativa das cadeiras é zero também, porque a velocidade angular das cadeiras é constante.
Vamos fazer uma observação importante: no termo correspondente à aceleração de coriolis () não podemos usar a velocidade angular da plataforma, temos que fazer o produto vetorial com a mesma velocidade angular que usamos para achar a velocidade relativa:
)

Então, ao invés de usarmos a aceleração de Coriolis, vamos usar essa expressão aí de cima.
Então, nossa equação vai ficar:
Já sabemos que:
Então:
Vamos resolver os produtos vetoriais:
E:
Vamos ter que: