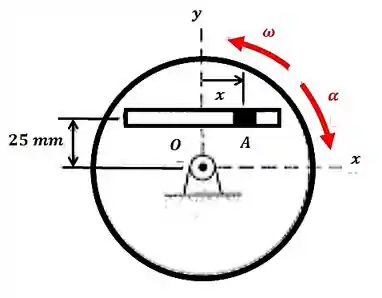
O disco gira em torno de um eixo fixo através de com velocidade angular e aceleração angular no instante representado, nos sentidos indicados. O cursor se desloca na ranhura reta. Determine a velocidade e a aceleração absolutas de para o mesmo instante, quando , e .
Passo 1
Nosso primeiro passo é identificar onde ocorre o movimento relativo. Perceba que enquanto o disco gira em torno de , o cursor se move na ranhura. Então, o movimento relativo ocorre no cursor . Para a velocidade vamos usar a seguinte equação:
Repare que o disco apenas gira em torno do ponto , ou seja, só possui velocidade angular com relação a esse ponto, então:
A velocidade angular é sempre perpendicular à figura, ou seja, está no eixo . Como ela faz o disco girar no sentido anti-horário, a velocidade angular é positiva de acordo com a nossa convenção de sinais:
E o vetor posição ? Ela indica a posição do cursor medido a partir do eixo no instante mostrado na figura:
A velocidade relativa é a velocidade do cursor com relação ao eixo que gira:
Então, vamos ter que:
Vamos resolver esse produto vetorial aí:
Substituindo isso aí na nossa equação, vamos ter que:
Então, será:
Passo 2
Agora vamos fazer a análise da aceleração. Para isso, vamos usar a seguinte equação:
Lembra que vimos que o corpo não tinha velocidade no ponto , portanto ele também não terá aceleração:
A aceleração angular do disco estará sempre no eixo e como ela gira no sentido contrário da velocidade angular, ela é negativa:
Repare que os vetores posição , velocidade angular e velocidade relativa não mudam:
Já a aceleração relativa é a aceleração que o cursor possui e está posicionada no eixo :
Então, vamos ter que:
Vamos fazer cada produto vetorial separado:
- Já sabemos que:
- :
- :
- :
Pronto! Agora é só substituirmos:
Somando os termos de mesma componente, obtemos: