Enquanto a ponte giratória está fechando com uma velocidade angular de , um homem corre ao longo da pista a uma velocidade constante de , relativamente à pista. Determine a velocidade e a aceleração do homem, no instante em que .
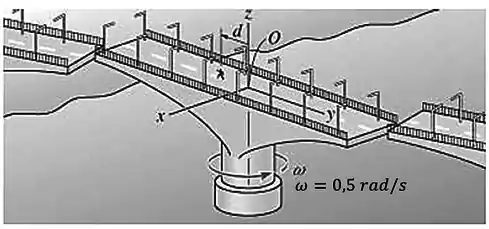
Passo 1
Como se trata de corpos que realizam movimentos de rotação e translação ao mesmo tempo, vamos utilizar a seguinte equação para a velocidade:
Nosso próximo passo é identificar onde ocorre o movimento relativo. Perceba que enquanto a ponte gira, o homem se move por ela. Então, o homem que realiza o movimento relativo. Agora vamos organizar a nossa equação.
A velocidade é a velocidade absoluta de quem realiza o movimento, que no nosso caso é o homem:
Essa é a primeira coisa que precisamos descobrir!
A velocidade é a velocidade da ponte. Mas repare que a ponte apenas gira, então a sua velocidade é zero:
A velocidade angular da ponte foi dada, mas repare que ela gira no sentido anti-horário, então o vetor é positivo:
O vetor posição do homem com relação ao eixo será:
E enfim, a velocidade relativa é a velocidade que o homem tem com relação a ponte. Repare que ele está correndo no sentido negativo do eixo :
Passo 2
Agora que identificamos o que é cada coisa na nossa equação, é só substituirmos:
Vamos resolver o produto vetorial separado:
Substituindo isso aí na nossa equação, vamos ter que:
O módulo da velocidade vai ser:
Passo 3
Agora vamos fazer a análise da aceleração. Para isso, vamos usar a seguinte equação:
A aceleração do homem é:
Lembra que vimos que a ponte não tem velocidade, portanto ela também não terá aceleração:
A aceleração angular da ponte também é zero, porque ela gira a velocidade constante:
Repare que os vetores posição , velocidade angular e velocidade relativa não mudam.
A aceleração relativa também é zero, porque o homem corre com velocidade constante :
Então, vamos ter que:
Já sabemos que:
Então:
Esse produto vetorial vai ficar:
O outro produto vetorial que precisamos é:
Substituindo isso na nossa equação, vamos ter:
O seu módulo será: