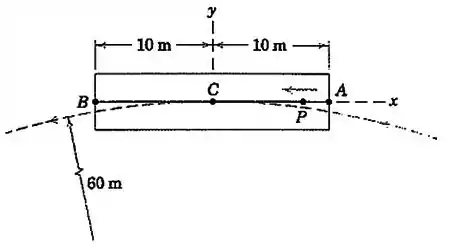
Ao contornar uma curva sem inclinação lateral a uma velocidade constante de , o centro do vagão ferroviário segue uma trajetória circular de raio . O eixo longitudinal do vagão permanece tangente ao círculo. Determine a velocidade absoluta de uma pessoa que caminha na velocidade constante de 1,5 m/s em relação ao vagão quando ele está nos pontos e . Utilize os eixos presos ao vagão como indicado.
Passo 1
Quando temos o movimento relativo de corpos que realizam movimento de rotação e translação ao mesmo tempo, vamos usar a seguinte equação:
O próximo passo é identificar quem está realizando o movimento relativo. Neste caso, é a pessoa. Então, a velocidade corresponde a velocidade absoluta da pessoa:
E é justamente o que queremos saber!
A velocidade é a velocidade absoluta do trem:
Que passando para , temos:
Como o trem anda para a esquerda, o vetor velocidade será:
Como o trem está realizando um movimento circular, a sua velocidade angular pode ser calculada assim:
Sabemos que a velocidade angular está sempre no eixo e como o trem está andando para a esquerda, então a velocidade angular é positiva:
E a velocidade relativa é a velocidade da pessoa com relação ao vagão do trem. Repare que a pessoa caminha da direita para a esquerda, ou seja, no sentido negativo do eixo :
Passo 2
Vamos calcular primeiro a velocidade absoluta da pessoa quando ela está no ponto . Repare que quando ela está no ponto , a sua posição é:
Então, a nossa equação fica:
Vamos resolver o produto vetorial:
Então:
Passo 3
Agora, vamos calcular a velocidade absoluta da pessoa quando ela está no ponto . Repare que quando ela está neste ponto, a sua posição é:
Então, a nossa equação fica:
Vamos resolver o produto vetorial:
Então:
Passo 4
Por último vamos calcular a velocidade absoluta da pessoa quando ela está no ponto . Repare que quando ela está neste ponto, a sua posição é:
Então, a nossa equação fica:
Essa é moleza, né?