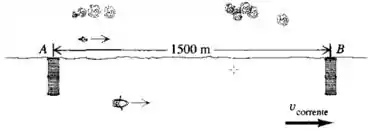
Dois píers estão localizados em um rio: o píer está situado a de correnteza abaixo, como na figura. Dois amigos devem fazer um percurso do píer ao píer e depois voltar. Um deles vai de barco com velocidade constante de em relação à água. O outro caminha pela margem do rio com velocidade constante de . A velocidade do rio é igual a no sentido de para . Calcule o tempo de cada um para fazer o percurso de ida e volta.
Passo 1
Vamos começar calculando o tempo que o amigo faz caminhando. Basta usar a equação de velocidade média. Se sua velocidade é constante ela é igual a velocidade média.
O percurso de ida e volta tem o dobro da distância entre o píer e o píer .
Nesse problema usamos e em vez de e porque é mais fácil, nesse caso, passar a distância para , do que passar a velocidade de para .
Passo 2
Vamos achar agora o tempo do amigo que faz o percurso de barco.
Devemos achar o tempo da ida e o tempo da volta do percurso. Para isso precisamos da velocidade do barco na ida e na volta.
- IDA:
- VOLTA:
Passo 3
Vamos achar agora o tempo que ele demora a ir do píer ao píer .
Passo 4
Vamos agora achar a velocidade do barco na volta.
A velocidade do barco é negativa porque ele está indo para esquerda.
Passo 3
Vamos achar agora o tempo que ele demora a ir do píer ao píer .
O é negativo porque ele se desloca para esquerda.
Passo 4
O tempo total será,