Uma pessoa está dentro de um elevador panorâmico que sobe com velocidade constante. Em um dado instante ela joga uma maçã verticalmente para cima pegando-a na mesma altura (em relação ao elevador) que a jogou. Um observador do lado de fora do elevador, em repouso, observa o movimento. Considerando sempre as quantidades observadas pela pessoa do lado de fora do elevador: o tempo que a maçã leva para atingir a altura máxima ; o intervalo de tempo contado a partir da altura máxima até a pessoa pegar a maçã ; o módulo da velocidade com que a maçã deixa a mão da pessoa e o módulo da velocidade que ela tem ao ser apanhada de volta . Assinale a alternativa correta.
(a) e
(b) e
(c) e
(d) e
(e) e
(f) e
Passo 1
Primeiro, vamos entender o que está acontecendo.
O elevador sobe com velocidade constante que chamaremos de , então, temos que a pessoa e a maçã estão paradas com relação a ele. Porém, se considerarmos um observador em repouso do lado de fora, ele estará vendo todos os três (elevador, pessoa e maçã) com a mesma velocidade .
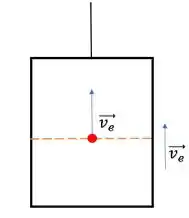
Agora, vamos pensar na pessoa lançando a maçã para cima e pegando-a na descida dentro do elevador.
Passo 2
Vamos analisar as velocidades de saída e de chegada da maçã com relação ao observador externo.
Para a maçã ser lançada para cima dentro do elevador, a pessoa impulsionou a maçã dando a ela uma velocidade para cima que chamaremos de .
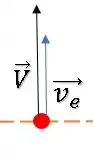
Então, o módulo da velocidade de saída com relação à pessoa de fora será a soma das duas velocidades:
Porém, quando a maçã retorna à mesma altura, ela terá a mesma velocidade de saída (em módulo), só que apontando para baixo.
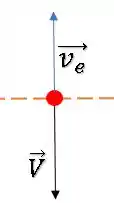
Então, o módulo da velocidade de chegada com relação à pessoa de fora será o módulo da subtração entre elas:
Descobrimos, assim, que (saída) vai ser necessariamente maior que (chegada).
Passo 3
Agora, vamos olhar para o tempo para atingir a altura máxima e o tempo para recuperar a partir da altura máxima .
Caso o nosso referencial fosse o próprio elevador, o movimento seria exatamente o de um lançamento vertical para cima. O tempo de subida seria e o de descida seria , sendo seus valores iguais.
Além disso, a altura máxima com relação ao elevador será atingida quando a velocidade da maçã volta a ser igual à do elevador .
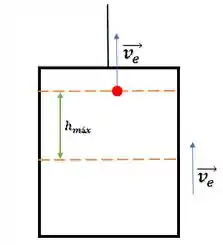
Mas se mudarmos o referencial, nesse instante, a maçã ainda estará subindo para o observador externo. Por isso, ela ainda estará alcançando a altura máxima, ou seja, dentro de .
Repare que inclusive quando ela começa a descer (dentro do elevador), a maçã ainda estará subindo para o observador externo, já que sua velocidade resultante ainda é para cima.
Então dá uma olhada na figura:
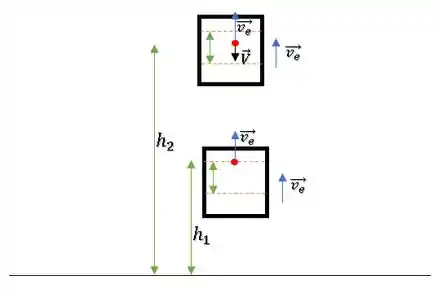
O tempo ainda está sendo contabilizado enquanto a maçã já está em movimento de descida (dentro do elevador). Então, podemos dizer que independente da velocidade inicial , o tempo para alcançar a altura máxima será maior do que o tempo para a pessoa recuperá-la a partir da altura máxima.
Ficamos com a alternativa (c).
Resposta
Letra (c)