No mecanismo de três barras mostrado, a haste de controle possui uma velocidade angular no sentido anti-horário durante um curto intervalo de movimento. Quando a haste ultrapassa a posição vertical mostrada, o ponto possui as coordenadas e . Determine por meio da álgebra vetorial as velocidades angulares de e .
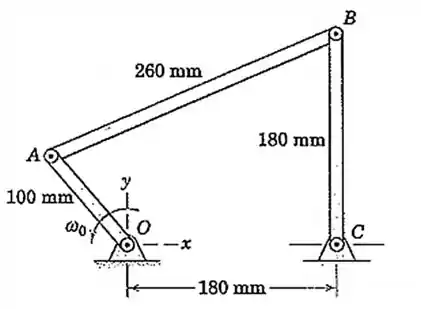
Passo 1
Vamos começar pela barra , pois sabemos a sua velocidade angular. Repare que o ponto gira em torno do ponto , então podemos escrever:
Sabemos que a velocidade angular da barra é no sentido anti-horário, então ela é positiva:
E o vetor posição ?
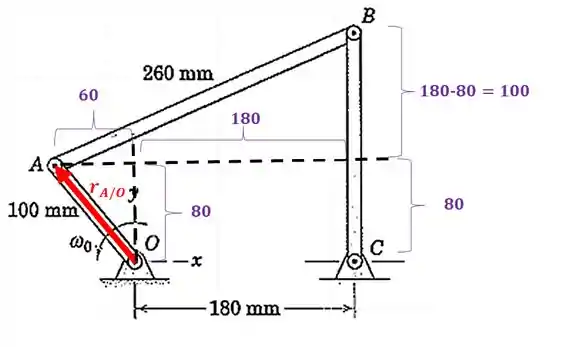
Ao decompor o vetor , temos:
Repare que a origem do eixo está em cima do ponto !!!
Então, vamos ter que:
Esse produto vetorial fica assim:
Então:
Passo 2
Agora vamos analisar a barra . Repare que o ponto gira em torno do ponto , então:
Nós não sabemos a velocidade angular da barra , então vamos arbitrar o sentido positivo:
E a posição é:
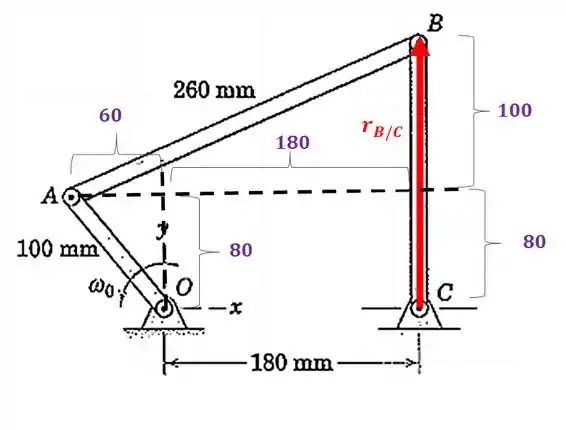
Vamos ter que:
Fazendo o produto vetorial vamos ter:
Passo 3
Agora vamos analisar a barra :
A velocidade angular da barra nós não sabemos, mas vamos arbitrar o sentido como positivo (anti-horário):
A posição é:
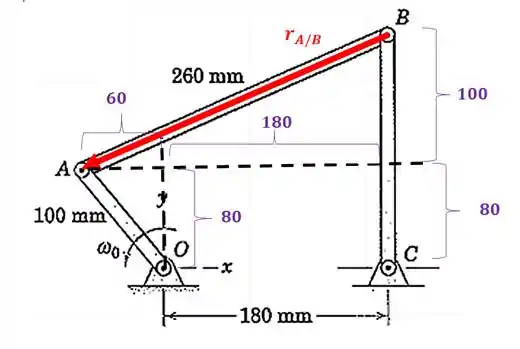
Agora vamos substituir o já temos:
O produto vetorial fica:
Então:
Agora vamos somar os termos da mesma componente:
Da equação em temos que:
Como achamos um valor positivo, significa que arbitramos o sentido certo para :
Agora vamos usar a equação das componentes em :
Como achamos um valor positivo, significa que arbitramos o sentido correto para :