02) A figura ao lado ilustra um mecanismo constituído por um aro fixo de raio e dois discos, um de centro A, raio e massa , e outro de centro B, raio e massa . Ambos os discos são articulados a uma treliça AOB de massa desprezível, que por sua vez é articulada no centro O do aro. O dispositivo assim construído mantém os discos em contato permanente com a superfície interna do aro, sendo C e D, respectivamente, os pontos de contato do disco de centro A e do disco de centro B com o aro. Sabendo que ambos os discos realizam movimento de rolamento sem escorregamento, pede-se:
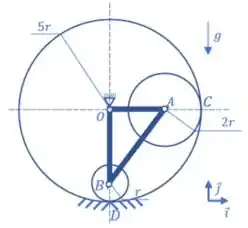
a) A relação onde é a velocidade angular do disco de centro A e é a velocidade angular do disco de centro B.
b) Os momentos de inércia do disco de centro A em relação ao polo C e do disco de centro B em relação ao polo D, nesta ordem.
c) Sabendo que o mecanismo parte do repouso quando . Determine a velocidade angular do disco de centro A no instante em que .
Passo 1
Eaí galerinhaaa, tudo tranquilo com vocês?
a) Temos uma questão bem interessante que começa trabalhando bastante a ideia do rolamento sem escorregamento. Nesse item precisamos determinar a relação entre as velocidades angulares dos discos de centro A e B. Mas, de qual equação da mecânica que vai sair essa razão?

Bom, na realidade a ideia é usar mais de uma equação buscando relacionar os discos A e B. Observando a estrutura podemos perceber que o primeiro ponto que tem seu movimento relacionado com esses dois discos é o centro O. Por isso, vamos tentar escrever sua velocidade (que é nula, pois é um ponto fixo) em função de e .
Sabemos que, como os discos A e B rolam sem escorregamento, os pontos C e D, respectivamente, possuem velocidade nula. Assim:
Massa! Sendo a velocidade angular da treliça, como A e B pertencem à treliça a gente pode escrever que:
Beleza, igualando agora as expressões que temos para e teremos:
Muito bom, estamos quase terminando. Agora é só igualar as duas expressões que temos para o :
Prontinho 😉
Passo 2
b) Nesse item devemos calcular o momento de inércia do disco A e do disco B em relação aos pontos C e D, respectivamente. O que pode causar problema aqui é que os pontos C e D não estão no centro do disco, assim temos que usar o teorema dos eixos paralelos pra encontrar a resposta. Lembra o que ele diz:
Então vamos lá! O momento de inércia em relação ao eixo que passa pelo centro do disco vale:
Para o disco A, como , teremos:
Já para o disco B, como , teremos:
Show! Terminamos mais um item.
Passo 3
c) Agora precisamos determinar em um outro instante, após a treliça ter rotacionado um pouco.
Temos, basicamente, duas opções: tentar encontrar aceleração angular pra determinar a nova velocidade angular, ou usar os teoremas de energia. A primeira opção não é muito legal porque não conhecemos a diferença de tempo entre as situações. Então bora pra energia!
Pelo teorema da energia cinética, sabemos que:
Como a única força que está executando trabalho é a força peso, analisando a diferença de altura para o centro de cada um dos discos na nova posição, vem que:
Já para a variação de energia cinética, podemos escrever que:
Lembrando do resultado lá do item A, sabemos que (esse resultado vale em qualquer instante), daí substituindo:
Igualando esse resultado ao trabalho calculado anteriormente, temos:
Muito bommm! Todo mundo conseguiu entender direitinho? Bem legal essa questão né, já vamo aproveitar o embalo e ir pra próxima, galera 😉
Resposta
a)
b)
c)