03) Um pequeno anel de massa move-se sem atrito sobre um arame cuja forma é definida pela equação vetorial:
No instante o anel parte com velocidade da posição mais elevada da curva, ou seja, correspondente a . Pede-se:
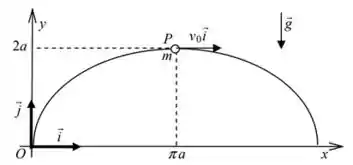
a) desenhar o diagrama de corpo livre do anel em uma posição genérica , indicando as componentes tangencial e normal da sua aceleração;
b) utilizando o diagrama de corpo livre do item a) escrever as equações do movimento do anel projetadas nas direções normal e tangencial;
c) determinar a velocidade do anel no instante em que se encontrar na posição correspondente a .
Passo 1
Ooii pessoal, tudo tranquilo por aí?
Bora dar o gás nessa questão!
Basicamente, temos um anel de massa que se movimenta em um arame que possui equação da curva definida.
a) Pra começar, devemos desenhar o diagrama de corpo livre (DCL) do anel para .
Bom, a primeira pergunta que nos fazemos é: quais forças atuam no anel nesse movimento?

Temos a força Peso, é claro, mas há também uma força normal devido ao contato do anel e do arame.
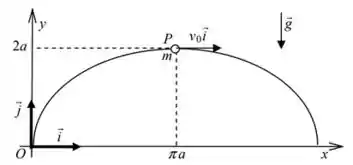
É falado no enunciado que, quando temos Assim, se , o anel está do lado direito do arame. Isso é importante pra saber qual a direção da força normal.
Sabendo dessas coisas, podemos desenhar:
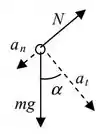
Prontinho!
Passo 2
b) Aqui devemos escrever as equações de força no anel em duas direções, a tangencial e a normal ao movimento. Vamos olhar novamente o DCL que desenhamos no item a).
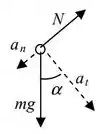
Tomando a componente do peso na direção tangencial, temos:
Já no sentido normal, temos:
Mas lembra que a em um movimento plano, podemos dizer que:
Onde e são funções de .
Ainda podemos melhorar um pouco nossas expressões lembrando do Triedo de Frenet.

Calma galera hahaha. É só a gente usar o vetor tangencial de Frenet. Como o é a direção entre o versor tangencial e o versor , podemos afirmar que:
Só que:
Maaaas,
Daí, simplificando tudo, temos:
Onde são funções de . E:
Show! Como o enunciado também não deixou muito claro em função do que queria as equações, essa resposta está ótima 😊
Passo 3
c) Devemos determinar a velocidade do anel quando
Como conhecemos a altura e velocidade iniciais, e temos apenas uma força que realiza trabalho (o peso), é uma ótima ideia usar o teorema da energia cinética.
Aplicando entre o instante inicial e o instante em que , temos:
Mas, qual que é a altura quando ?

O bizu é olhar pra equação do vetor posição:
A altura é justamente a componente em . Logo, para temos:
Substituindo, temos:
Aeee, prontinhoo! Matamos mais uma questão.
Até a próxima galeraaa, tamo junto 😉
Resposta
a) Resolução no texto.
b) Resolução no texto.
c)