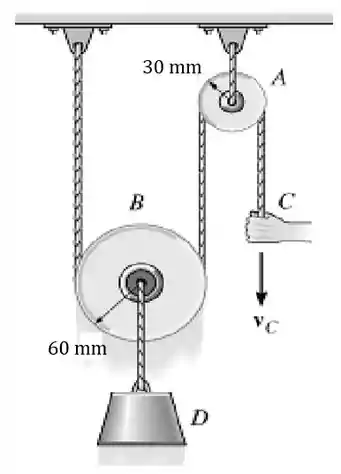
Se a extremidade da corda está sendo puxada com velocidade , determine as velocidades angulares das polias e e a velocidade do bloco . Suponha que a corda não escorregue nas polias.
Passo 1
Vamos analisar a polia primeiro. Repare que esta polia está presa, ou seja, ela só pode girar em torno do seu e centro. Então, vamos usar a equação do movimento de rotação:
Qual é a velocidade que a polia () possui? Nesses problemas admitimos que as cordas são inextensíveis, ou seja, elas não variam de comprimento nem nada. Então, a velocidade por toda a corda é a mesma:
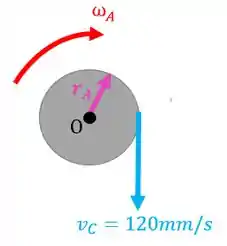
Então, podemos escrever que:
O que queremos saber é a velocidade angular da polia , então:
Vamos ter:
Repare que não precisa pssar o raio para metros, porque a velocidade foi dada em !!!
Passo 2
Agora vamos analisar a polia . Repare que esta polia não está presa, então ele sofre rotação e deslocamento. Quando temos uma polia nesta situação, temos que usar o nosso esquema:
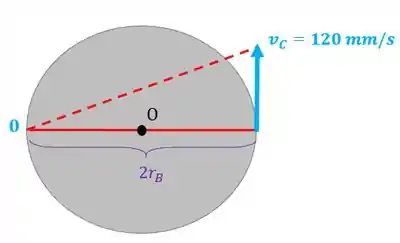
Mas sabemos que a velocidade por toda a corda é a mesma, então:
Podemos reescrever nossa equação assim:
Pronto, agora é só substituir os valores:
Passo 3
Está faltando acharmos a velocidade com que o bloco sobe:
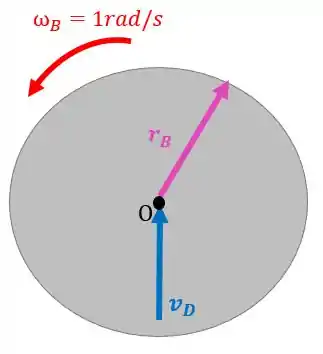
Para achar vamos usar os dado que temos do movimento da polia :