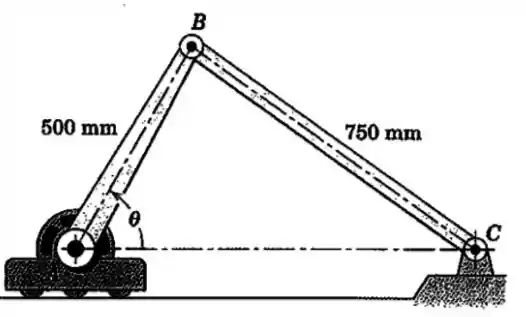
A unidade consiste em um motor com redução de alto torque que gira a barra na taxa constante . A unidade é livre para se mover ao longo da superfície horizontal. Determine a velocidade da unidade quando atinge .
Passo 1
Vamos entender o que está acontecendo... Conforme o ângulo aumenta, o ponto se move para a direta.
Então, vamos ter que:
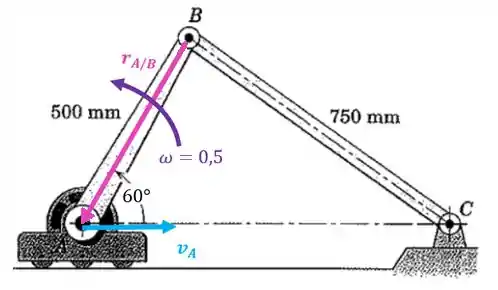
Vamos achar o vetor primeiro, lembrando que:
Para isso, temos que decompor :
E o vetor fica sempre no eixo Falta saber se ele é positivo ou negativo. Mas é só olhar como ele faz a barra girar, que no nosso caso é no sentido anti-horário, ou seja, é positivo:
Pronto! Podemos fazer o produto vetorial:
Então:
Seu módulo será:
O vetor fica assim:
Passo 2
Vamos agora analisar o vetor . Repare também que o ponto tende a girar em torno do ponto fixo , de modo que a velocidade neste ponto é tangente à trajetória circular
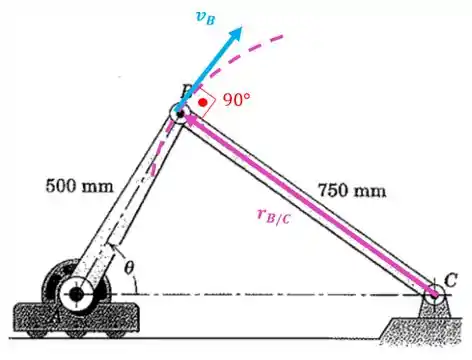
Repare que para achar a velocidade do ponto , teríamos que achar a velocidade relativa da barra :
Isso daria muito trabalho... Então, vamos usar a lei dos senos:
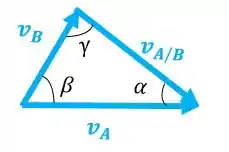
Mas antes temos que achar esses ângulos entre os vetores. Vamos começar pelo ângulo que o vetor faz com a horizontal:
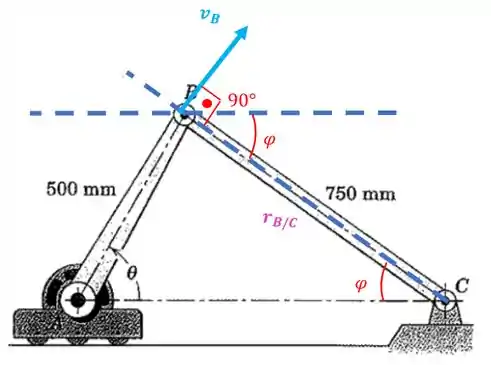
Repare que o ângulo que o vetor faz com a horizontal vai ser:
Podemos achar quanto vale o ângulo pela geometria inicial do nosso problema e utilizando a lei dos senos também:
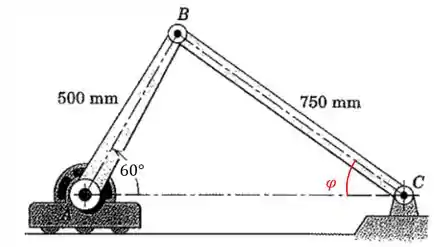
Então, este ângulo vai ser:
Podemos achar o valor de :
Agora vamos achar o ângulo que o vetor faz com relação a horizontal:
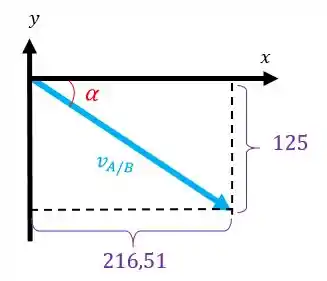
Então, já temos até agora:
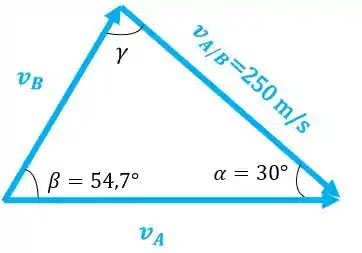
O ângulo será:
Agora podemos aplicar a lei dos senos para achar o valor de :
O vetor aponta no sentido positivo do eixo , então podemos escrever o vetor como: