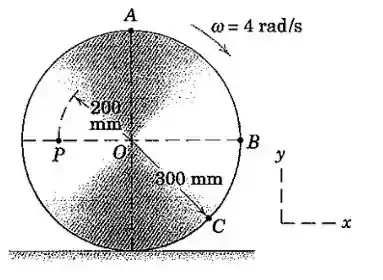
O disco circular rola sem deslizar com uma velocidade angular no sentido horário . Para o instante representado, escreva as expressões vetoriais para a velocidade de com relação a e para a velocidade de .
Passo 1
Primeiro, vamos achar a velocidade de com relação a :
A velocidade angular está sempre no eixo . Mas qual é o seu sinal? Repare que a velocidade angular faz o disco girar no sentido horário e este sentido foi o que estabelecemos como negativo:
Repare também que a velocidade angular é a mesma para todos os pontos que pertencem ao disco:
Beleza?
Falta acharmos o valor de :
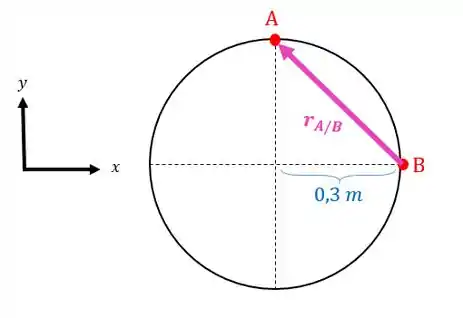
Não se esqueça que o vetor vai ter sua origem no ponto e vai chegar no ponto , já que o exercício quer a velocidade de com relação a . ![]()
Como vamos fazer um produto vetorial, vamos decompor o vetor :
Agora é só substituirmos:
Vamos montar nossa matriz para fazer o produto vetorial:
Então, a velocidade de com relação a :
Passo 2
Agora vamos achar a velocidade do ponto . Repare que o ponto gira em torno do ponto que é o centro do círculo:
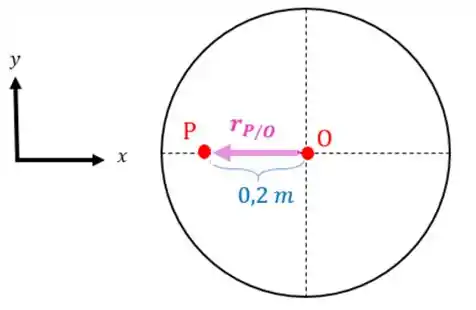
Vamos ter que:
Onde:
Vamos fazer esse produto vetorial. Sabendo que:
Então:
E a velocidade do ponto ()? Como o círculo anda para a direita, então o sentido da velocidade do ponto é:
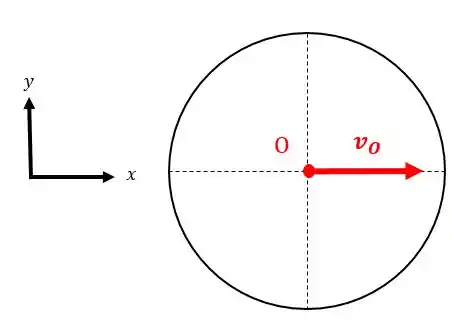
Agora é só usarmos a fórmula da rotação para achar o seu módulo:
Então, a velocidade do ponto será: