A extremidade da barra possui uma velocidade para baixo de durante um intervalo de seu movimento. Para a posição em que determine a velocidade angular de e a velocidade do ponto central da barra. Resolva as equações da velocidade relativa, inicialmente utilizando geometria do polígono de vetores e, em seguida, utilizando a álgebra vetorial.
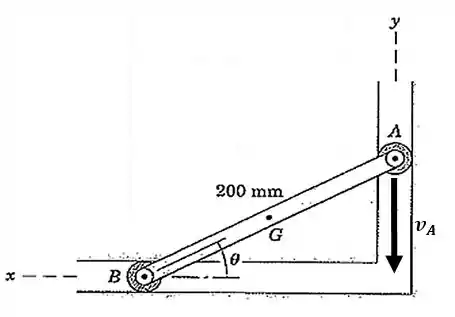
Passo 1
Quando a extremidade se move para baixo, a extremidade da mesma barra se move para a esquerda:
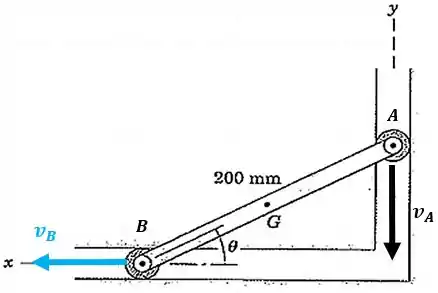
Sabemos que a velocidade angular é calculada da seguinte forma:
Então, a velocidade angular da barra será:
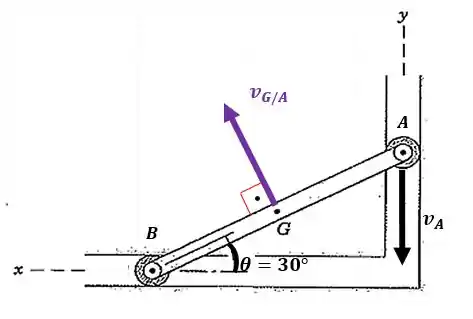
Mas como calcular a velocidade de com relação a ? Para achar seu valor vamos ter que fazer uma soma dos vetores velocidade que temos. Mas lembre-se que a velocidade relativa é sempre perpendicular à linha que une os dois pontos, ou seja, no nosso caso o vetor vai ser perpendicular a barra :
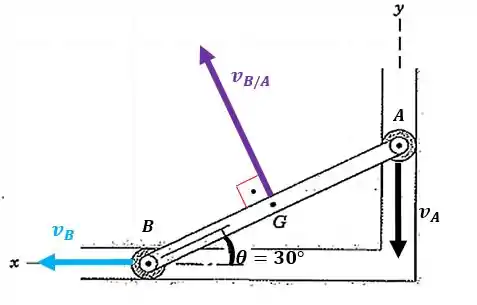
O triângulo de velocidades fica assim:
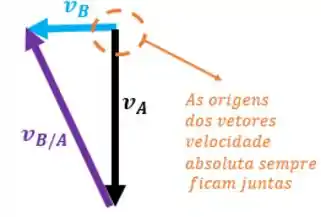
Agora vamos achar os ângulos entre os vetores:
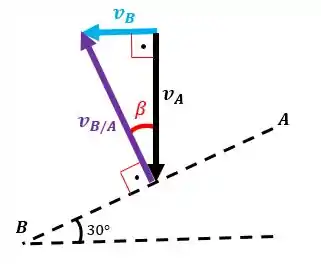
Para achar o ângulo temos que fazer a seguinte sequência:
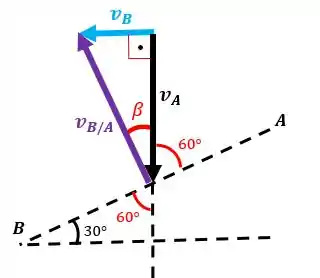
Então, será:
A velocidade do ponto nós temos e vale , então:
Com esse valor podemos calcular a velocidade angular da barra :
Para determinar o sinal da velocidade angular usamos a regra da mão direita: temos que colocar os quatro dedos da palma da mão direita no sentido do vetor e com isso o seu dedão vai apontar para o sentido positivo do eixo (para dentro da tela). Ou seja, a velocidade angular faz a barra girar no sentido horário:
O sentido horário é positivo devido a posição do eixo !!!
Passo 2
Agora temos que calcular a mesma coisa do passo anterior, porém de forma vetorial. Para isso, vamos usar a equação da velocidade relativa. Temos que a velocidade da extremidade é:
O vetor posição de em relação a quando é:
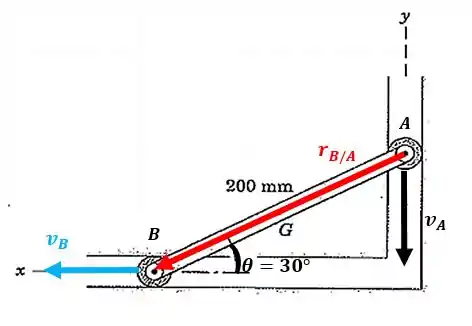
Sabemos que o vetor é:
O vetor aponta no sentido positivo do eixo e podemos calcular o seu valor através do triângulo de velocidades:
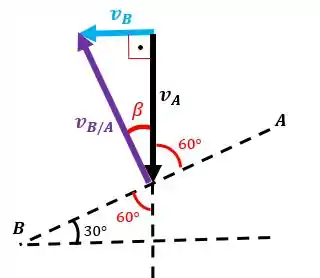
Então, o vetor é:
Como estamos fazendo de conta que não sabemos o valor da velocidade angular, podemos dizer apenas que:
Depois vamos descobrir se é positivo mesmo ou negativo.
Passo 3
Vamos substituir o que temos na equação da velocidade:
Nosso produto vetorial vai ficar:
Então:
Somando os termos da mesma componente:
O valor de é:
Como encontrado antes!!!
Passo 4
Agora vamos achar o valor da velocidade do ponto central da barra utilizando o triângulo de velocidades.
Sabemos que o vetor velocidade relativa de com relação a é perpendicular à reta que liga os pontos e :
Então, o triângulo de velocidades vai ficar:
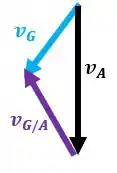
Temos o mesmo ângulo entre os vetores:
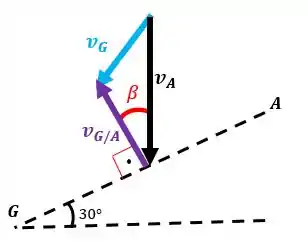
Repare que podemos calcular , pois já sabemos a velocidade angular da barra:
Agora para saber o valor de é só usarmos a lei dos cossenos:
Passo 5
Agora vamos calcular a velocidade utilizando a equação da velocidade:
O vetor posição será:
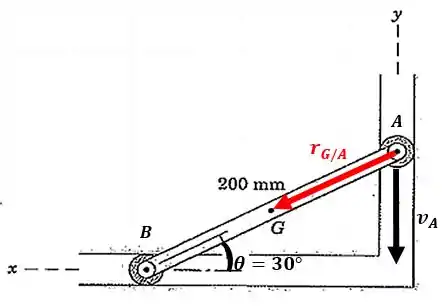
Então, o vetor vai ser:
E seu módulo é: