O mecanismo mostrado na figura foi desenvolvido para dar à lâmina presa no cursor um golpe lento e retornar rapidamente. Determine a velocidade do cursor no instante em que , se a barra gira a .
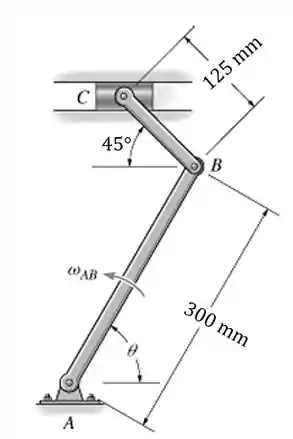
Passo 1
Primeiro vamos entender o que está acontecendo. A barra está girando em torno do ponto fazendo com que a barra se mova. O que queremos saber é a velocidade no ponto . Então, o nosso diagrama cinemático fica assim:
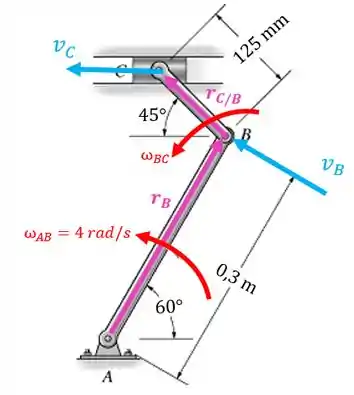
Calma, vamos analisar cada barra separadamente. Mas qual devemos analisar primeiro? A barra que tenha sido dada alguma informação sobre ela na questão. No nosso caso é a barra . Repare que o ponto realiza um movimento circular em torno do ponto :
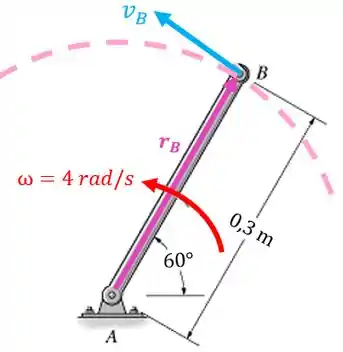
Repare que o vetor velocidade é tangente à trajetória. Como o movimento de é somente de rotação em torno de , vamos usar a equação do movimento de rotação:
Passo 2
Precisamos fazer o produto vetorial, então vamos decompor o vetor em relação ao eixo :
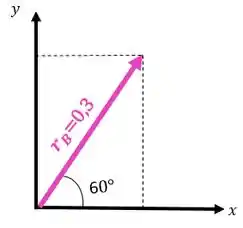
Sabemos que a velocidade angular tem apenas uma componente no eixo só falta sabermos se ela aponta para o sentido positivo ou negativo deste eixo. Lembra que definimos que quando a velocidade angular gira no sentido anti-horário ela é positiva? Como está girando neste sentido, ela é positiva:
Nosso produto vetorial vai ficar assim:
Para resolver o produto vetorial é só lembrar que para cada componente é só excluir a linha e a coluna correspondente. Se for por exemplo a componente no eixo :
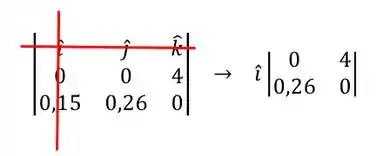
Agora é só acharmos os determinantes dessas matrizes :
Então, a velocidade no ponto será:
Passo 3
Agora vamos fazer nossa análise para a barra :
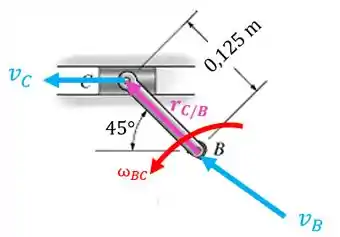
Vamos ter que:
Sendo que a velocidade relativa do ponto com relação ao ponto () é:
Vamos decompor o raio :
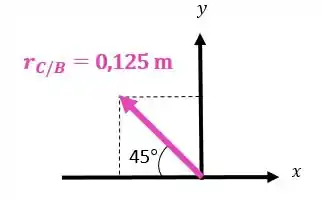
A aceleração angular da barra também gira no sentido anti-horário, ou seja, ela é positiva:
Então, vamos ter o seguinte produto vetorial:
Que pode ser escrito assim:
A velocidade será:
Passo 4
Agora que sabemos a velocidade relativa de com relação a e o valor de vamos substituir na equação para achar :
Teremos:
Mas repare que o cursor só pode se mover na horizontal, de modo que a sua velocidade será:
Então, podemos escrever:
Agora é só somarmos todos os termos de mesma componente ( com e com ) . Vamos ter o seguinte sistema:
E:
De cara podemos achar o valor de pela segunda equação:
Substituindo isso na primeira equação:
O vetor velocidade do ponto vai ser:
Como o sinal deu negativo, significa que a velocidade aponta no sentido negativo do eixo .